三角関数
1.直角三角形での定義
直角三角形のイメージ
直角三角形なので、\(0 < \theta < \pi/2 \)となる。
\(\sin\theta = \frac{c}{a}, \quad \quad \cos\theta = \frac{b}{a}, \quad \quad \tan\theta=\frac{c}{b}\) \(\sec\theta=\frac{1}{\cos\theta},\quad \cot\theta=\frac{1}{\tan\theta}\)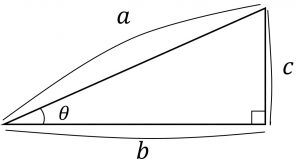
ピタゴラスの定理:\(a^2+b^2=c^2\)
別名:三平方の定理
この定理から以下が成り立つ。
\(\sin^2\theta + \cos^2\theta = 1\) \(1+\tan^2\theta = \frac{1}{\cos^2\theta}\)
2.単位円での定義
角度\(\thetaが\pi/2\)以上になると、直角三角形が作れない。
そこで\(xy\)平面上で半径1の円(単位円)を考えて定義しなおす。
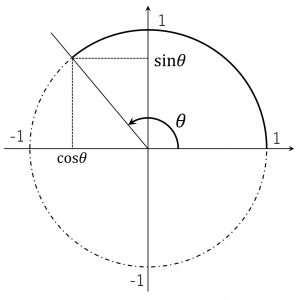
単位円に定義しなおす事で、角度\(\theta\)の時の円上の点の\(x座標の値が\cos\theta,y座標の値が\sin\theta\)となります。
\(\theta\)は任意の実数の値。
\(\tan\theta=\frac{\sin\theta}{\cos\theta}\) \(\sin(-\theta) = -\sin\theta,\quad \cos(-\theta) = \cos\theta\) \(\tan(-\theta)=-\tan\theta\) \(\sin ( \theta+\frac{\pi}{2} ) = \cos\theta, \quad \cos ( \theta+\frac{\pi}{2} ) = -\sin\theta\) \(\tan ( \theta+\frac{\pi}{2} ) = \large{-\frac{1}{\tan\theta}}\) \(\sin(\theta + \pi) = -\sin\theta,\quad \cos(\theta+\pi) = -\cos\theta\) \(\tan(\theta+\pi)=\tan\theta\)上記の三角関数の関係式を導くための、”ざっくり”とした考え方です。(※厳密には値で考えてください。)
単位円と\(\theta と\cos\theta,\sin\theta\)の正負について

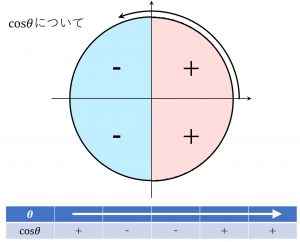
となります。
\(\sin(\theta +\frac{\pi}{2})\)の正負について考えると、
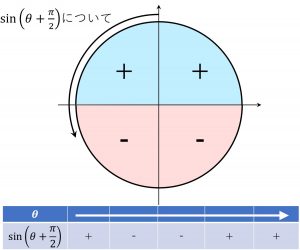
\(\cos\theta\)と同じ正負の進み方である事がわかる。
なので、\(\sin(\theta +\frac{\pi}{2})=\cos\theta\)です。
(※厳密には値で考えてください。)
3.正弦定理
\(\triangle ABC\)の外接円の半径を\(R\)とすると、下記の公式が成り立つ。
\( \large{\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R}\)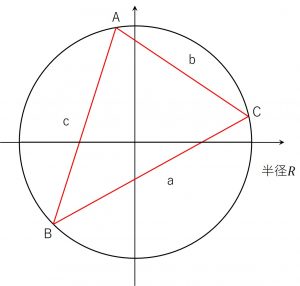
(1).\(A\)が鋭角のとき
\(BDが\triangle ABC \)の外接円の直径となるように点\(D\)をとる。
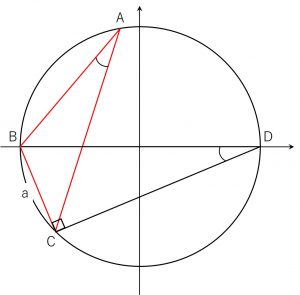
円周角の定理から、\(\angle BDC = A , \angle DCB = 90^{ \circ }\)であり、\(BD=2R\)となる。
\(a = 2R\sin\angle BDC = 2R\sin A\)
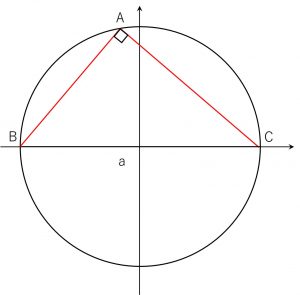
(2).\(A\)が直角のとき
(3).\(A\)が鈍角のとき
\(BDが\triangle ABC \)の外接円の直径となるように点\(D\)をとる。
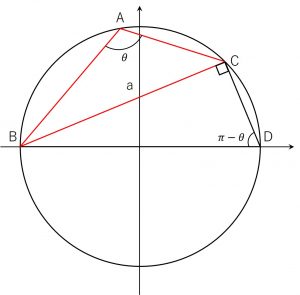
円周角の定理から、\(\angle BDC = \pi – A , \angle DCB = 90^{ \circ }\)であり、\(BD=2R\)となる。
\(a = 2R\sin\angle BDC = 2R\sin (\pi – A)= 2R\sin A \)
(1) ~ (3) から
\(a=2R\sin A \)\(b,c\)についても同じ証明が出来るので、
\( \large{\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R}\)
4.余弦定理
\(\triangle ABC\)について、下記の公式が成り立つ。
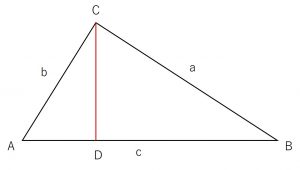
\(a^2=b^2+c^2-2bc\cos\angle A\) \(b^2=c^2+a^2-2ca\cos\angle B\) \(c^2=a^2+b^2-2ab\cos\angle C\)\(\triangle ABC\)について、点CからABに垂線を下ろし交わった点をDとする。
↓
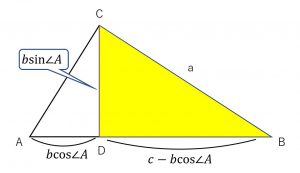
のように各辺の長さが分かる。
この各辺の長さと、黄色の三角形(\( \triangle BCD\))についての三平方の定理から、
余弦定理を求める。
\(\begin{align} BC^2 &= CD^2 + DB^2 \\ a^2 &= (b\sin\angle A)^2 + (c-b\cos\angle A)^2 \\ &= b^2(\cos^2 \angle A + \sin^2 \angle A ) +c^2 -2bc \cos^2 \angle A \\ &= b^2 +c^2 -2bc\cos \angle A \end{align}\)
5.加法定理と倍角の公式
三角関数について、以下の公式が成り立つ。
\(\sin(\alpha + \beta) = \sin\alpha \cos\beta + \sin\beta \cos\alpha\) \(\cos(\alpha + \beta) = \cos\alpha \cos\beta – \sin\alpha \sin\beta\) \(\tan(\alpha + \beta) = \frac{\tan\alpha + \tan\beta}{1-\tan\alpha \tan\beta}\)座標\((x,y)を(x’,y’)\)へ角度αだけ回転移動させる操作は、行列を用いて以下のように表される。
\(\left( \begin{array}{c} x’ \\ y’ \end{array} \right) = \left( \begin{array}{cc} \cos\alpha & -\sin\alpha \\ \sin\alpha & \cos\alpha \end{array} \right)\left( \begin{array}{c} x \\ y \end{array} \right)\)さらに座標\((x’,y’)を(x”,y”)\)へ角度βだけ回転移動させる操作は、行列を用いて以下のように表される。
\(\begin{align}\left( \begin{array}{c} x” \\ y” \end{array} \right) &= \left( \begin{array}{cc} \cos\beta & -\sin\beta \\ \sin\beta & \cos\beta \end{array} \right)\left( \begin{array}{c} x’ \\ y’ \end{array} \right) \\ &= \left( \begin{array}{cc} \cos\beta & -\sin\beta \\ \sin\beta & \cos\beta \end{array} \right) \left( \begin{array}{cc} \cos\alpha & -\sin\alpha \\ \sin\alpha & \cos\alpha \end{array} \right)\left( \begin{array}{c} x \\ y \end{array} \right) \\ &= \left( \begin{array}{cc} \cos\alpha \cos\beta-\sin\alpha\sin\beta & -(\sin\alpha\cos\beta + \sin\beta\cos\alpha) \\ \sin\alpha\cos\beta + \sin\beta\cos\alpha & \cos\alpha \cos\beta-\sin\alpha\sin\beta \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right) \end{align}\)これは座標\((x,y)を(x”,y”)\)へ角度(α+β)だけ回転移動させる操作と同じなので
\(\left( \begin{array}{c} x” \\ y” \end{array} \right) = \left( \begin{array}{cc} \cos(\alpha + \beta) & -\sin(\alpha + \beta) \\ \sin(\alpha + \beta) & \cos(\alpha + \beta) \end{array} \right)\left( \begin{array}{c} x \\ y \end{array} \right)\)と先ほどの式を比べると
\(\sin(\alpha + \beta) = \sin\alpha \cos\beta + \sin\beta \cos\alpha\)\(\cos(\alpha + \beta) = \cos\alpha \cos\beta – \sin\alpha \sin\beta\)
が成り立つことがわかる。
\(\tan(\alpha+\beta)\)について
\(\begin{align} \tan(\alpha + \beta) &= \large{\frac{\sin(\alpha + \beta)}{\cos(\alpha+\beta)}} \\ &= \large{\frac{\sin\alpha \cos\beta + \sin\beta \cos\alpha}{\cos\alpha \cos\beta – \sin\alpha \sin\beta}} \\ &= \large{\frac{\frac{\sin\alpha \cos\beta}{\cos\alpha \cos\beta}+\frac{\sin\beta \cos\alpha}{\cos\alpha \cos\beta}}{1-\frac{\sin\alpha \sin\beta}{\cos\alpha \cos\beta}}} \\ &= \large{\frac{\tan\alpha + \tan\beta}{1-\tan\alpha \tan\beta}} \end{align}\)(※\(\alphaと\betaが\pi/2\)の時も、成り立ちます。)
加法定理に\(\alpha=\theta,\beta=\theta\)を代入すれば求められる。
\(\sin2\theta = 2\sin\theta\cos\theta\) \(\begin{align} \cos2\theta &= \cos^2\theta – \sin^2\theta \\ &= 2\cos^2\theta -1 \\ &= 1-2\sin^2\theta \end{align}\) \(\tan2\theta = \large{\frac{2\tan\theta}{1-\tan^2\theta}}\)
6.その他
\(\cos\)の倍角の公式から得ることが出来る。
\(\sin^2\frac{\theta}{2} = \frac{1-\cos\theta}{2}\) \(\cos^2\frac{\theta}{2} = \frac{1+\cos\theta}{2}\) \(\tan^2\frac{\theta}{2} = \frac{1-\cos\theta}{1+\cos\theta} \)
加法定理から三角関数の積の公式が得られる。
\(\sin\alpha\cos\beta = \frac{1}{2}[ \sin(\alpha + \beta) +\sin(\alpha – \beta) ]\) \(\cos\alpha\cos\beta = \frac{1}{2}[ \cos(\alpha + \beta) +\cos(\alpha – \beta) ]\) \(\sin\alpha\sin\beta = -\frac{1}{2}[ \cos(\alpha + \beta) -\cos(\alpha – \beta) ]\)
三角関数の積の公式から\(\alpha + \beta = A , \quad \alpha – \beta = B\)と置いて整理すると
\(\sin A + \sin B = 2\sin ( \frac{A+B}{2} ) \cos ( \frac{A-B}{2} )\) \(\cos A + \cos B = 2\cos ( \frac{A+B}{2} ) \cos ( \frac{A-B}{2} )\)