数列と収束
0.数列と収束
自然界には、規則的に変化する現象がある。
それらの現象を理解するには数列の理解が不可欠である。
また数学では無限和、無限積で定義される関数や現象がある。
それらの関数、現象を扱うには
・どのような範囲
・どのような値
・最終的に行きつく値
を知る必要が出てくる。
1.数列
ある規則に従って並べられた数の列の事。
— 一般的な表し方 —
\( a_1,a_2,a_3,\cdots ,a_n,\cdots \)
または
\( \{ a_n \} \)
で表す。
また、\( a_1 \)を初項、\( a_2 \)を第2項
と呼び、\( a_n \)を第\( n \)項または一般項と呼ぶ。
数列は自然数で定義されることが多いが、稀に \(a_{-3} \) 等、整数で定義されることもある。
上記でも述べたように、数列とは規則に従って並べられた数の列だが、
明確な場合
\( a_n = 5n ,\quad a_n = a_{n-1} r +2 ,\quad a_n = n^2\)
のように数式で表す。これを一般項と呼ぶ。
以下によくみられる数列を示す。
・等差数列
\( a_1 = a_1 ,\quad a_2 = a_1 +d ,\quad a_3 = a_1 + 2d , \cdots \cdots \)
・等比数列
\( a_1 = a_1 , \quad a_2 = a_1 r , \quad a_3 = a_1 r^2 , \cdots \cdots \)
・階差数列
ある数列 \( {b_n} \) がある時、この数列を差とする数列
\( a_1 = a_1 , \quad a_2 = a_1 + b_1 ,\quad a_3 = a_1 + b_1 + b_2 , \cdots \cdots \)
2.漸化式
以前の項との関係式を示す数列式の事。
上記で示した数列を漸化式で示してみる
・等差数列
\( a_n = a_{n-1} + d \)
・等比数列
\( a_n = a_{n-1} r \)
・階差数列
\( a_n = a_{n-1} + b_{n-1} \)
有名な漸化式では、フィボナッチ数列がある。
・フィボナッチ数列
\( a_1 = 1, \quad a_2 =1,\quad a_n = a_{n-1} + a_{n-2} \)
以下に、漸化式を数種類紹介しておく。
① 階差数列の形 \( a_{n+1} – a_n = f(n) \)
\begin{eqnarray} a_{n} = a_1 +\sum_{k=1}^{n-1} f(k) \quad (n \ge 2) \end{eqnarray}
② \( a_{n+1} = f(n)a_n \)
\begin{eqnarray} a_n = f(n-1)f(n-2) \cdots f(2)f(1)a_1 \end{eqnarray}
③ \( a_{n+1} = p a_n + q \quad (n=1,2,3,\cdots \cdots , ; p \neq 1,\quad q \neq 0 ) \)
\( \alpha = p \alpha + q \) となる \( \alpha \) をとり、各辺を引くと
\( a_{n+1} – \alpha = p(a_n – \alpha) \)
と表せられるので、数列{ \( a_n – \alpha \) } は
\( 公比p,\quad 初項(a_1 – \alpha) \) の等比数列となる
ゆえに、
\( a_n -\alpha = (a_1 -\alpha)p^{n-1} \)
④ \( a_{n+1} = pa_n + g(n) \quad (p \neq 0 ) \)
両辺を \( p^{n+1} \) で割ると、
\( \frac{a_{n+1}}{p^{n+1}} – \frac{a_n}{p^n} = \frac{g(n)}{p^{n+1}} \)
ここで、 \( c_n = \frac{a_n}{p^n} \) , \( f(n) = \frac{g(n)}{p^{n+1}} \) と置くと
\( c_{n+1} – c_n = f(n) \) となり①の方法で解ける。
① \( a_1 = 1,\quad a_{n+1}=\frac{n}{n+1} a_n \) の数列 \( a_n \) を求めよ。
② \( a_1 = 1,\quad a_{n+1} = 3a_n + 2 \) の数列 \( a_n \) を求めよ。
③ \( a_1 = 1,\quad a_{n+1} = 3a_n + 3^{n+1} \) の数列 \( a_n \) を求めよ。
例題①).
\( a_n = \frac{n-1}{n}a_{n-1} \)
\( a_n = \frac{n-1}{n} \frac{n-2}{n-1} a_{n-2} \)
\( a_n = \frac{n-1}{n} \frac{n-2}{n-1}\frac{n-3}{n-2} \cdots \cdots \frac{1}{2} a_1 = \frac{1}{n} \)
例題②).
\( \alpha = 3\alpha +2 \) を与式から引くと、
\( a_{n+1} – \alpha = 3(a_n – \alpha) \)
\( a_{n+1} = 3a_n – 2\alpha \) となり、与式と比較して、 \( \alpha = -1 \)
つまり、
\( a_{n+1} +1 = 3(a_n +1) \)
となり、 \( \{ a_n +1 \} \) の数列の初項は 2 、公比は 3 とわかるので、
\( a_n +1 = 2\cdot 3^{n-1} \)
∴ \( a_n = 2\cdot 3^{n-1} -1 \)
例題③).
両辺を \( 3^{n+1} \) で割り、 \( c_n = \frac{a_n}{3^n} \) と置くと
\( c_{n+1} = c_n + 1 \)
つまり、
\( c_n = c_1 + \sum_{k=1}^{n-1} 1 \)
\( c_n = \frac{1_1}{3} + (n-1) = n-\frac{2}{3} \)
よって、 \( c_n = \frac{a_n}{3^n} \) なので、
\( a_n = 3^n (n-\frac{2}{3}) \)
3.数列の和
数列の和 \( a_1 + a_2 + \cdots \cdots +a_n \) を \( \displaystyle \sum_{k=1}^{n} a_k \) と書く。
— 性質 —
(1). \( \displaystyle \sum_{k=1}^{n} (a_k + b_k) = \sum_{k=1}^{n} a_k + \sum_{k=1}^{n} b_k \)
(2). \( \displaystyle \sum_{k=1}^{n} c a_k = c \sum_{k=1}^{n} a_k \)
(3). \( \displaystyle \sum_{k=1}^{n} c = nc \)
※ \( c \) は定数。
(1). \( \displaystyle \sum_{k=1}^{n} k = 1 + 2 + \cdots + n = \frac{n(n+1)}{2} \)
(2). \( \displaystyle \sum_{k=1}^{n} k^2 = 1^2 + 2^2 + \cdots + n^2 = \frac{n(n+1)(2n+1)}{6} \)
(3). \( \displaystyle \sum_{k=1}^{n} k^3 = 1^3 + 2^3 + \cdots + n^3 = \{ \frac{n(n+1)}{2} \}^2 \)
(4). \( \displaystyle \sum_{k=1}^{n} k^4 = 1^4 + 2^3 + \cdots + n^4 \) \( = \frac{1}{30}n(n+1)(2n+1)(3n^2+3n-1) \)
\( \displaystyle \sum_{k=1}^{n} (k+1)^3-k^3 \) の値を2通りの計算をする事で証明する。
\begin{eqnarray} \sum_{k=1}^{n} \{ (k+1)^3-k^3 \} &=& \sum_{k=1}^{n} ( k^3+3k^2+3k+1-k^3 ) \\ &=& \sum_{k=1}^{n}(3k^2+3k+1) \\ \end{eqnarray}
ここで左辺と右辺について、別々に式変形をする。
\begin{eqnarray} 左辺 &=& (2^3-1^3)+(3^3-2^3)+(4^3+3^3)+ \cdots +((n+1)^3+n^3) \\ &=& -1^3 + (2^3 – 2^3)+(3^3-3^3)+\cdots + (n^3-n^3) +(n+1)^3 = (n+1)^3-1 \\ \end{eqnarray} \begin{eqnarray} 右辺 &=& \sum_{k=1}^{n}(3k^2+3k+1) = \sum_{k=1}^{n} 3k^2 +\sum_{k=1}^{n} 3k + \sum_{k=1}^{n} 1 \\ &=& 3 \sum_{k=1}^{n} k^2 + 3\frac{1}{2}n(n+1) +n \\ \end{eqnarray}
次に、右辺=左辺として再計算して、目的の二乗の和を求める。
\begin{eqnarray} 3 \sum_{k=1}^{n} k^2 + \frac{3}{2}n(n+1) +n &=& (n+1)^3-1 \\ 3 \sum_{k=1}^{n} k^2 &=& (n+1)^3 – \frac{3}{2}n(n+1) – (n+1) \\ &=& \frac{(n+1)}{2} \{ 2(n+1)^2 -3n -2 \} \\ &=& \frac{(n+1)}{2}(2n^2 +n) \\ &=& \frac{1}{2}n(n+1)(2n +1) \\ \sum_{k=1}^{n} k^2 &=& \frac{1}{6}n(n+1)(2n +1) \\ \end{eqnarray}
となる。
— 他の累乗の和について —
同様に、3乗の和については
\( (k+1)^4 – k^4 \) の和について計算を行う
4乗の和については
\( (k+1)^5 – k^5 \) の和について計算を行う事で求めることが出来る。
この形になる数列の和の問題が多い。
4.数列の収束
数列\( {a_n} \) が与えられ、\( n \to \infty \) にした時、
特定の実数値 \( \alpha \) に近づくならば、
\[ \lim_{n \to \infty} a_n = \alpha \]
と書き、\( a_n \) は \( n \) を無限大に飛ばした時、
\( \alpha \) に収束するという。
上記の収束の説明は厳密ではない。
何故なら、
・無限大に飛ばすとは?
・無限大とはどれくらい大きくするのか?
・どんな値よりも大きい数?
・じゃあそれより大きい数では?
等と、無限大( \( \infty \) )とは非常に抽象的な表現である。
この収束を具体的に説明した証明法が下記で示す
\( \varepsilon – N \) 論法である。
極限を議論するのに、用いらられる証明法である。
「 \( \lim_{n \to \infty } a_n = \alpha \) 」
これを \( \varepsilon – N \) 論法で書き直すと、
↓
「\( \forall \varepsilon , \exists N \in \mathbb{N} \quad s.t. \quad \forall n > N \to |a_n – \alpha | < \varepsilon \)」
関連 >> 数学記号と意味
数学の記号が多くて、よくわからない方もいるかと思うので、
記号を使わずに答えると、
「任意の\(\varepsilon\)に対して、もし\( n \)が\( N \)より大きいなら、\( |a_n – \alpha | < \varepsilon \) となる\( N \)が存在する。」
日本語に直しても分かりにくいですよね。
これを説明していきます。
「\( \forall \varepsilon , \exists N \in \mathbb{N} \quad s.t. \quad \forall n > N \to |a_n – \alpha | < \varepsilon \)」
この論法の厳密な所は、極限を議論するのに具体的に
「ものすごく大きな数字 ( \( n \) )」
と
「ものすごく小さな数字 ( \( \varepsilon \) )」
を設定できたところです。
では、どの辺りが設定できているのか解説していきます。
1. \( \exists N \in \mathbb{N},\quad \forall n > N \)
・特定の\( N \)
・それより大きい全ての\( n \)
大きい数の議論
A「ものすごく大きい\( N \)よりも大きい数字?」
B「いつでもAさんが考える数字\( N \) よりも大きい数字 \( n \) だよ」
これでもの凄く大きな数字を設定できた。
2. \( \forall \varepsilon > 0 \)
・0より大きい全ての\( \varepsilon \)
小さい数の議論
A「0より大きいかったら、どんだけ小さくてもいいの?」
B「どんだけ小さくてもいいですよー」
これでものすごく小さい数を設定できた。
※厳密には大きい数字も含んでいる。
ただこの論法で意味するところは、
めっちゃ小さい数を扱うという事です。
3. \( |a_n – \alpha | < \varepsilon \)
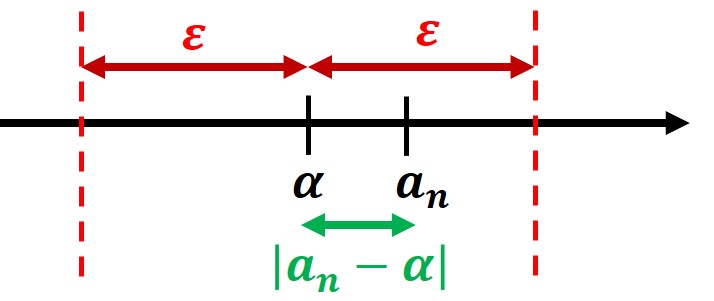
・\( \alpha \) を中心に距離 \( \varepsilon \) 内に \(a_n \) が存在する。
収束の議論
A「ものすごく小さい\( \varepsilon \) 内に \( a_n \)があるの?」
B「そうだよ」
A「じゃあ\(a_n\)ってほぼほぼ\(\alpha\)じゃん」
このように厳密に大きい数と小さい数を議論できるのが、\( \varepsilon – N \) 論法です。
そのため極限を議論出来るのです。
関連 >> \( \varepsilon – \delta \)論法 (関数の極限)
5.無限級数の収束性
無限数列\( {a_n} \)の各項を初項から無限に足し合わせた式を無限級数という。
\begin{align} a_1 + a_2 + \cdots + a_n + \cdots = \sum_{k=1}^{\infty} a_k \end{align}
無限数列\( {a_n} \)の各項を初項から無限に足し合わせた式を無限級数という。
無限級数が\( S \)に収束する時、
\begin{align}
\sum_{n=1}^{\infty} a_n = S
\end{align}
と表す。
(1). 数列\( {a_n} \)の無限級数が収束する時、
\begin{align}
\lim_{n \to \infty } a_n = 0
\end{align}
数列\( {a_n} \)は0に収束する。
(2) . 数列\( {a_n} \)が収束する時、無限級数\( \lim_{n \to \infty}S_n\)は収束するとは限らない。
(1)の証明
\( \sum_{n \to 1}^{\infty} a_n \)が\(S\)に収束する時、\( n \ge 2 \)で
\begin{align}
a_n = S_{n} – S_{n-1}
\end{align}
であるから
\begin{align}
\lim_{n \to \infty } a_n &= \lim_{n \to \infty } (S_{n} – S_{n-1}) \\
&= S-S \\
&=0
\end{align}
(2)の例
\begin{align}
a_n = 1 + \frac{1}{n}
\end{align}
この数列\( a_n \)は\( \lim_{n \to \infty } a_n = 1 \)と収束するが、その級数は
\begin{align}
\sum_{n=1}^{\infty} 1 + \frac{1}{n} = \infty
\end{align}
と発散する。