ε – δ 論法
1.ε-δ論法
・解析学に置いて、実数値を用いて極限を議論する方法。
・19世紀に発案。
・関数の極限を厳密に議論する際によく使う。
下記からは、数学記号を多用するので、
次のページを参考にしてください。
関連 >> 数学記号と意味
\[ \lim_{x \to a} f(x) = b \]
↓ \(\varepsilon – \delta \) 論法で書き直し
\[ \forall \varepsilon > 0 , \exists \delta > 0 \quad s.t. \quad \forall x \in \mathbb{R} , 0 < | x-a | < \delta \to |f(x)-b| < \varepsilon \]
と表せる。
これの意味は、
任意の\( \varepsilon ( \forall \varepsilon ) \) に対して、\(\delta \)が存在する( \( \exists \delta \) )。
どのような\( \delta \)か( \( s.t. = such \quad that \)以下説明)というと、
もし\( |x-a| < \delta \) ならば、\( |f(x)-L| < \varepsilon \) となるような \( \delta \)。
そのまま読んでみました。
分かりやすい文にします。
「任意の \( \varepsilon \) に対して、もし\( |x-a| < \delta \) ならば、\( |f(x)-L| < \varepsilon \) となるような \( \delta \)が存在する。 」
「この時 \(\lim_{x \to a} f(x) = b \) となる事が証明できる。」
私はこの式を見て、眠たくなりました。
みなさんも頑張って
\[ \forall \varepsilon > 0 , \exists \delta > 0 \quad s.t. \quad \forall x \in \mathbb{R} , 0 < | x-a | < \delta \to |f(x)-b| < \varepsilon \]
ある任意の正の数 \( \varepsilon \) を決めると、適当な \( \delta \) が存在する、という事だ。
そして、\( 0 < |x-a| < \delta \) を満たす全ての実数 \( x \) に対し、\( |f(x) -b | < \varepsilon \)
が成り立つ。
\( \varepsilon \) は有限の値だが、任意なので好きなだけ小さく選んでも良い。
少しだけ、具体的に考えてみる。
\( \varepsilon_1 \) に対応して、\( \delta_1 \) が存在し、
\[ 0 < |x-a| < \delta_1 \to |f(x)-b| < \varepsilon_1 \]
が成り立つ。
次に \( \varepsilon_2 (< \varepsilon_1) \) に対応して、\( \delta_2 \) が存在し、
\[ 0 < |x-a| < \delta_2 \to |f(x)-b| < \varepsilon_2 \]
が成り立つ。
この式に少し付け加えると、
\[ 0 < |x-a| < \delta_2 \to |f(x)-b| < \varepsilon_2 < \varepsilon_1 \]
となる。
そのため、ものすごい小さい \( \varepsilon ‘ \) 選び、
それに対応した \( \delta ‘ \) を決めておけば、
\( \varepsilon ‘ \) 以上の \( \varepsilon \) に関して、\( \delta ‘ \)
が成り立つ。
逆に、小さい \( \varepsilon \) で \( \delta \) が存在しなければ、
任意の \( \varepsilon \) に対して、適当な \( \delta \) が存在するという論理を満たさない。
これが極限を議論できる理由である。
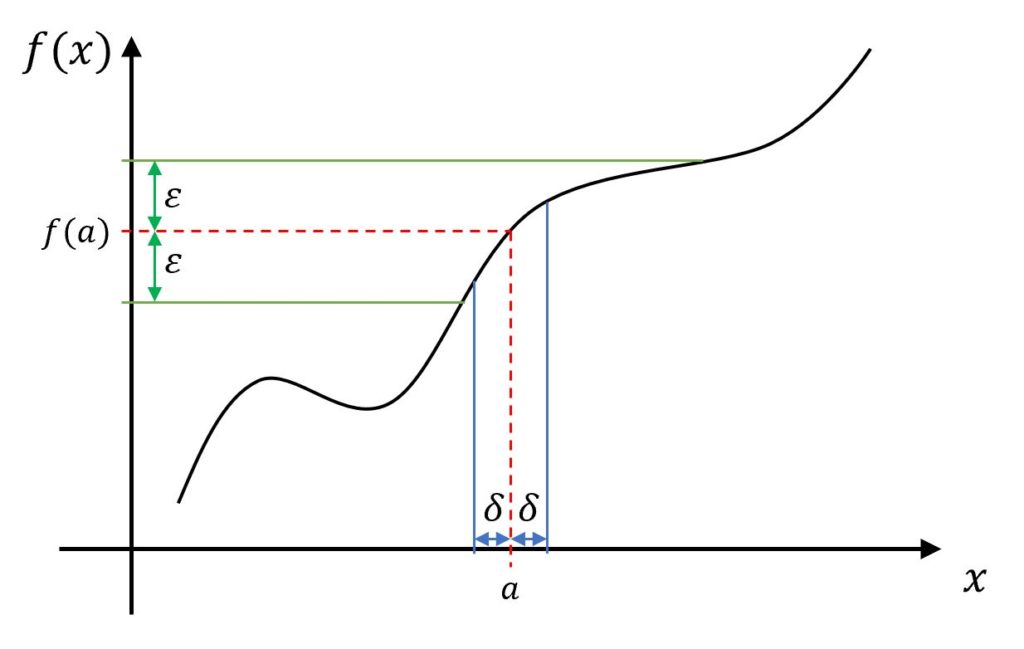
↓ \( \varepsilon \) を小さくしても成り立つ。
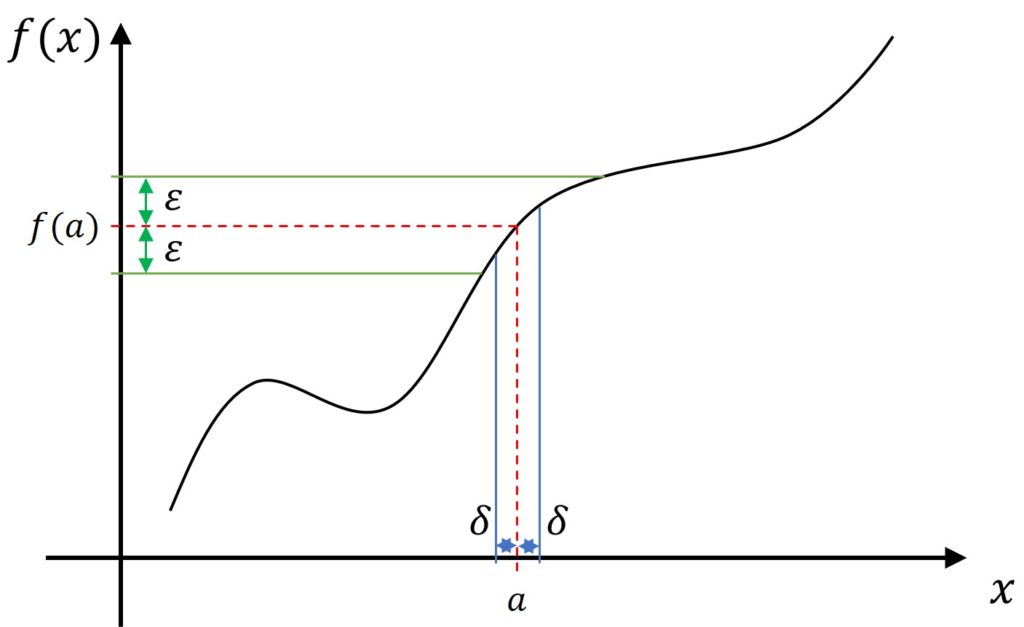
↓
どんなに小さな \( \varepsilon \) を考えても、
\( 0 < |x-a| < \delta \) ならば、\( |f(x) -b | < \varepsilon \)
になるような \( \varepsilon \) があるなら、
\[ \lim_{x \to a} f(x) = b \]
である。
2.ε-δ論法 (証明)
\( \varepsilon – \delta \) 論法で \( \lim_{x \to 2} ( 3x +1 ) = 7 \)
を証明せよ。
例).
\( \varepsilon – \delta \) 論法で書き直すと、
\[ \forall \varepsilon > 0 , \exists \delta > 0 , s.t. \forall x \in \mathbb{R} , 0 < |x-2| < \delta,\to |f(x)-7| < \varepsilon \]
となる。これを示す。
\( |x-2| < \delta \) であれば、
\begin{eqnarray}
| (3x+1) – 7 | &=& |3x-6| \\
&=& 3|x-2| \\
< 3 \delta
\end{eqnarray}
よって、
\begin{eqnarray}
3\delta &<& \varepsilon \\
\delta &<& \frac{\varepsilon}{3}
\end{eqnarray}
となる \( \delta \) をとれば、\( |f(x) -7 < \varepsilon| \) を満たす。
従って、\( \lim_{x \to 2} ( 3x +1 ) = 7 \) を示せた。
\( \varepsilon – \delta \) 論法で次の極限を証明せよ。
(1). \( \displaystyle \lim_{x \to 2} (x^2 + 3x) = 10 \)
(2). \( \displaystyle \lim_{x \to 1} \frac{1}{1+x} = \frac{1}{2} \)
例題1).
\( \varepsilon – \delta \) 論法で書き直すと、
\[ \forall \varepsilon > 0 , \exists \delta > 0 , s.t. \forall x \in \mathbb{R} , 0 < |x-2| < \delta,\to |f(x)-10| < \varepsilon \]
となる。これを示す。
\( | x-2 | < \delta \) であれば、
\begin{eqnarray}
| x^2 +3x -10 | &=& | (x-2)(x+5) | \\
&=& |x-2||x+5| \\
&=& |x-2||(x-2)+7|
& \leq & |x-2|(|x-2|+7)
\end{eqnarray}
ここで \( \delta = min(\frac{\varepsilon}{8} , 1) \) と置く。
\( min(a,b) \) は \(a,b\) どちらか小さい方を選ぶという事です。
つまり、\( |x-2| < \frac{\varepsilon}{8} \) と \( |x-2| < 1 \) が成り立つ
\begin{eqnarray}
|x^2+3x-10| & \leq & |x-2|(|x-2|+7) \\
& < & \frac{\varepsilon}{8}(1+1) \\
& = & \varepsilon
\end{eqnarray}
よって、任意の \( \varepsilon \) を決めれば、
\( \delta = min(\frac{\varepsilon}{8},1) \) と \( \delta \) を決めればよい。
与式の証明が出来た。
例題2).
\( \varepsilon – \delta \) 論法で書き直すと、
\[ \forall \varepsilon > 0 , \exists \delta > 0 , s.t. \forall x \in \mathbb{R} , 0 < |x-1| < \delta,\to |f(x)-\frac{1}{2}| < \varepsilon \]
となる。これを示す。
\( | x-1 | < \delta \) であれば、
\begin{eqnarray}
| \frac{1}{1+x} – \frac{1}{2} | &=& |\frac{1}{2}\frac{1-x}{1+x} | \\
&=& \frac{1}{2}|\frac{x-1}{x+1}|
\end{eqnarray}
ここで、下記の不等式を用いる。
\begin{eqnarray}
|1+x| + |1-x| & \geq & |(1+x) + (1-x) | = 2 \\
|x+1| & \geq & 2 – |x-1|
\end{eqnarray}
これを用いると、
\begin{eqnarray}
| \frac{1}{1+x} – \frac{1}{2} | &=& \frac{1}{2}|\frac{x-1}{x+1}|\\
& \leq & \frac{1}{2} \frac{|x-1|}{2-|x-1|} \\
\end{eqnarray}
となるので、
ここで \( \delta = min( \varepsilon , \frac{3}{2}) \) と置く。
\( min(a,b) \) は \(a,b\) どちらか小さい方を選ぶという事です。
つまり、\( |x-1| < \varepsilon \) と \( |x-2| < \frac{3}{2} \) が成り立つ
よって、
\begin{eqnarray}
| \frac{1}{1+x} – \frac{1}{2} | & \leq & \frac{1}{2} \frac{|x-1|}{2-|x-1|}\\
& < & \frac{1}{2} \frac{\varepsilon}{2-\frac{3}{2}} \\
& = & \varepsilon \\
\end{eqnarray}
よって、任意の \( \varepsilon \) を決めれば、
\( \delta = min(\varepsilon,\frac{3}{2}) \) と \( \delta \) を決めればよい。
与式の証明が出来た。
