整式の除法
1.整式の除法
xの整式\(A(x)、B(x)\)に対し
\(A(x) = B(x)Q(x) + R(x)\) \(ただし、(R(x)の次数)<(B(x)の次数)\)となる整式\(Q(x)、R(x)はただ1組定まる。\)
ここで\(Q(x)、R(x)をA(x)をB(x)\)で割った商、余りという。
2.剰余の定理・因数定理
整式\(f(x)\)について
① \(x-a\)で割った時の余りは\(f(a)\)に等しい。
② \(ax-b\)で割った時の余りは\(f(\frac{b}{a})\)に等しい。
整式\(f(x)\)について
① \(f(a)=0 \Longleftrightarrow f(x)はx-a\)を因数に持つ。
② \(f(-\frac{b}{a})=0 \Longleftrightarrow f(x)は ax+b \quad(a \neq 0)\)を因数に持つ。
③ \(f(\alpha )=f(\beta)=0 (\alpha \neq \beta)\)
\( \quad \quad \Longleftrightarrow f(x)は (x-\alpha)(x-\beta)\quad (a \neq 0)\)を因数に持つ。
④ \(f(x)が(x-\alpha)^2で割り切れる。\)
\( \quad \quad \Longleftrightarrow f(\alpha)=0\quad かつ \quad f'(\alpha)=0\)を\(x-\alpha\)で割った時、商を
\(\quad g(x) = b_0 x^{n-1} + b_1x^{n-2}+\cdots+b_{n-1}\)余りを\(R\)とすると
\(\quad f(x) = (x-\alpha)g(x)+R\)両辺の同次の項の係数をくらべて、
\(\quad a_0 = b_0,\quad a_1 = b_1 -b_0\alpha ,\quad \dots \quad ,a_n = R-b_{n-1}\alpha\)
3.最大公約数、最小公倍数
公約数の中で最も大きい数を最大公約数と言う。
例).24と42の最大公約数:6
例).84と102の最大公約数を求める。
① 下記のように、二つの数字を並べて公約数で割っていく。
② 公約数が1だけになるまで①を続ける。
③ 最後に左の数字を全てかけたものが最大公約数になる。

例).452と242の最大公約数を求める。
① 2つの数のうち、大きい数を小さい数で割る。
② ①で使った小さい数を、割った余りで割る。
③ ・・・わかりづらいので図で確認お願いします。
④ 割り切れる所まで行うと、最後に割った数が最大公約数になる。

最大公約数は36となります。
公倍数の中で0以外の最も小さい数を最小公倍数という。
例).8と12の最小公倍数:24
例).16と30の最小公倍数を求める。
① 下記のように数字を並べて、公約数で割っていく。
② 公約数が1になるまで①を続ける。
③ 最後に左の数字と、下の数字を全てかけたものが最小公倍数と言う。
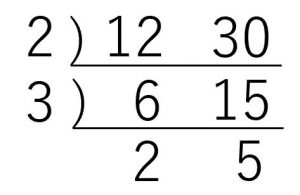
最小公倍数は\(2\times3\times2\times5 = 60\)
2つの整式\(A,Bの最大公約数をG、最小公倍数をLとすると\)
\(A=aG,\quad B= bG \quad (a,bは互いに素)\) \(L = abG,\quad LG=AB\)
4.分数式
① 分数式の分母、分子が公約数を持たない時、これを既約分数式という。
② 分数式の分母、分子をその公約数で割って簡単にすることを約分するという。
③ 分母の異なるいくつかの分数式で、分母を同じになるように変形することを通分するという。
① \( \frac{A}{B} = \frac{A\times C}{B\times C},\quad \frac{A}{B}=\frac{A\div C}{B\div C} \)
② \( \frac{A}{D} + \frac{B}{D} – \frac{C}{D} = \frac{A+B-C}{D}\)
③ \( \frac{A}{B} \times \frac{C}{D} = \frac{A\times C}{B \times D} \)
④ \( \frac{A}{B} \div \frac{C}{D} = \frac{A}{B} \times \frac{D}{C} \)
① 分子を分母で割る
\(\quad \quad \frac{x^2+1}{x-1} = x+1+\frac{2}{x-1}\quad\)など
② 部分分数に分解する。