高次方程式
1.高次方程式
高次方程式の解法
① 因数定理などを利用して因数分解する。
\quad f(x) = f_1(x)\cdot f_2(x) \cdot f_3(x) \quad と因数分解出来るとき
\quad f(X) =0 \Longleftrightarrow \begin{cases} f_1(x) = 0 \quad または \\ f_2(x) = 0 \quad または \\ f_3(x) = 0\end{cases}② 実数係数のn次方程式が虚数解a+biを持てば、必ずa-bi(共役複素数)を持つことを利用する。
2.高次不等式
高次不等式の解法
f(x) \gt 0 \quad or \quad f(x) \lt 0 \quadの形に整理し、
f(x)を因数分解して解を求める。(表やグラフを用いる。)
高次不等式の解
例).3次不等式の場合
(\alpha,\beta,\gammaを\alpha \lt \beta \lt \gammaの実数とする。)① (x-\alpha)(x-\beta)(x-\gamma)\gt 0の解は
\quad \alpha \lt x \lt \beta,\quad \gamma \lt x② (x-\alpha)^2(x-\beta) \lt 0 の解は
\quad x \lt \beta \quad (x \neq \alpha)例題1 (3次不等式)
x^3-3x^2-6x+8 \gt 0 \quad を解け
解答).
\begin{align} f(x) &= x^3-3x^2-6x+8 \\ &= (x+2)(x-1)(x-4) \end{align}
| x | -2 | 1 | 4 | ||||
| x+2 | – | 0 | + | + | + | + | + |
| x-1 | – | – | – | 0 | + | + | + |
| x-4 | – | – | – | – | – | 0 | + |
| f(x) | – | 0 | + | 0 | – | 0 | + |
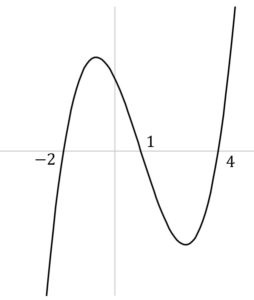
ゆえに
\quad -2 \lt x \lt 1,\quad 4 \lt 4
例題2 (4次不等式)
2x^4-9x^3+4x^2+21x-18 \lt 0 \quad を解け
解答).
f(x)=2x^4-9x^3+4x^2+21x-18とおくと、f(1)=0
である事から
\begin{align} f(x) &= 2x^4-9x^3+4x^2+21x-18 \\ &= (x-1)(2x^3-7x^2-3x+18) \\ &= (2x+3)(x-1)(x-2)(x-3) \end{align}
| x | -\frac{3}{2} | 1 | 2 | 3 | |||||
| 2x+3 | – | 0 | + | + | + | + | + | + | + |
| x-1 | – | – | – | 0 | + | + | + | + | + |
| x-2 | – | – | – | – | – | 0 | + | + | + |
| x-3 | – | – | – | – | – | – | – | 0 | + |
| f(x) | + | 0 | – | 0 | + | 0 | – | 0 | + |
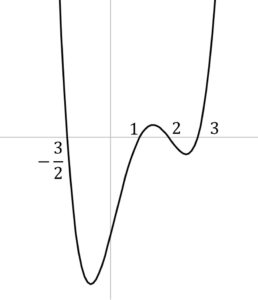
ゆえに
-\frac{3}{2} \lt x \lt 1 , \quad 2 \lt x \lt 3
3.2項方程式
2項方程式
x^n = a^nを二項方程式という。
必ずx=aを解としてもつので、因数分解すると
(x-a)(x^{n-1}+ax^{n-2}+a^2x^{n-3}+\cdots + a^{n-2}x + a^{n-1})=0となり、nが偶数のときはさらに、x=-aも解となる。
1の立方根
x^3 = 1の3つの解のこと。
x = 1が解の1つなので、
\quad x^3-1 = (x-1)(x^2+x+1) = 0 \quad ∴ x=1,\quad \frac{-1\pm\sqrt{3}i}{2}
\frac{-1+\sqrt{3}i}{2},\quad \frac{-1-\sqrt{3}i}{2}\quad を1の虚数立方根といい
一方を\omegaとすれば、他方は\omega^2となる。
\omega^2について
① \omega = \frac{-1+\sqrt{3}i}{2}とすると、
\quad \omega^2 = \frac{-2-2\sqrt{3}i}{4} = \frac{-1-\sqrt{3}i}{2}② \omega = \frac{-1-\sqrt{3}i}{2}とすると、
\quad \omega^2 = \frac{-2+2\sqrt{3}i}{4} = \frac{-1+\sqrt{3}i}{2}
