三角関数と図形
1.三角形の面積
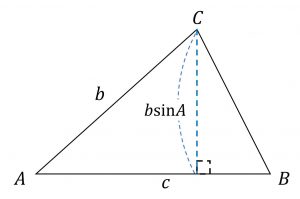
2辺と夾角が与えられている
\begin{align} S = \triangle ABC & = \frac{1}{2}bc \sin{A} \\ & = \frac{1}{2}ca \sin B \\ & = \frac{1}{2}ab \sin C \end{align}
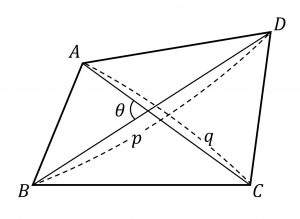
四角形の面積
四角形ABCDの対角線の長さをp.q,なす角の1つを\thetaとすると、
四角形ABCD = \frac{1}{2}pq \sin \theta
2.三角形の面積
三角形の面積
① 外接円の半径をRとすると
\quad \quad \large{S = \frac{abc}{4R} = 2R^2\sin A \sin B \sin C}② 内接円の半径をrとすると
\quad \quad \large{S = \frac{1}{2}r(a+b+c)}③ 3辺の長さが分かる時(ヘロンの公式)
\quad \quad S=\sqrt{s(s-a)(s-b)(s-c)}※s = \frac{1}{2}(a+b+c)
