1次関数
1.1次関数
1次関数とは
最大次数が1次の関数である。
1次関数の形
変化の割合 = \large{\frac{yの増加量 \quad }{xの増加量\quad }} = a
よく下記のように表される。
y = ax+bと表される時、yはxの1次関数と言われる。
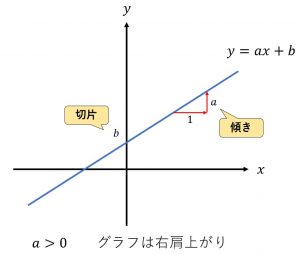
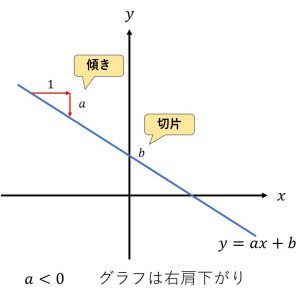
aは傾き、bは切片と言われる。
※a,bは定数である。xは変数である。
2.1次関数のグラフ
傾きについて
y=ax+bのグラフにおいて
a > 0の時、グラフは右肩上がり。
a \lt 0の時、グラフは右肩下がり。
3.1次関数の決定
1次関数の決定
① 1点と傾きが与えられたとき。
② 2点が与えられたとき。
例1).(1,2)を通り、傾きが3の1次関数を求める。
傾きが3なので、
y=3x+b(1,2)を通るので、
2=3\cdot 1+b \quad \to \quad b=-1よって問の求めたい1次関数は
y = 3x -1
例2).(-1,8) , (4,-7)を通る1次関数を求める。
傾きは
\frac{yの増加量 \quad}{xの増加量 \quad} = \frac{(-7)-(8)}{(4)-(-1)} = \frac{-15}{5} = -3つまり、傾きが-3の関数は
y=-3x+bと置ける。
(-1,8)を通るので、
8=-3\cdot (-1)+b \quad \to \quad b=5よって問の求めたい1次関数は
y = -3x +5
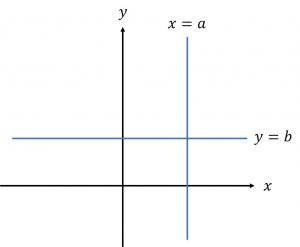
4.軸に平行な直線
軸に平行な直線
x=a,y=b,etc…
5.2直線の位置関係
平行の関係
2直線y=ax+bとy=a^{\prime}x+b^{\prime}がある時、
a=a^{\prime}の時、平行。a\neq a^{\prime}
