立体の表面積と体積
1.角柱・円柱の表面積と体積
角柱・円柱の表面積と体積
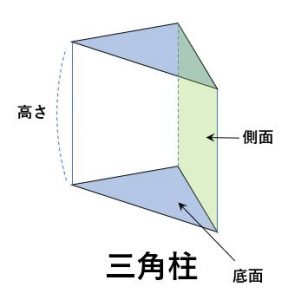
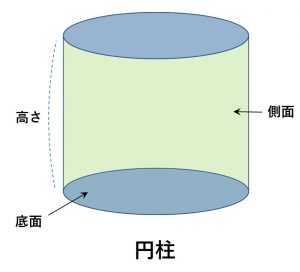
底面の面積を底面積。側面全体の面積を側面積と言う。立体全体の表面全体の面積を表面積という。
① \(角柱・円柱の表面積=底面積\times2+側面\)
② \(角柱・円柱の表面積=底面の周の長さ\times高さ\)
③ \(角柱・円柱の体積=底面積\times高さ\)
例).3辺の長さが\(a,b,c\)の直方体がある。この直方体の表面積と体積を求める。
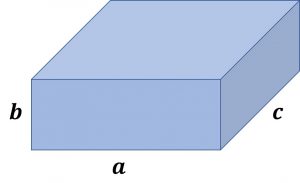
\(体積=底面積\times 高さ=ac\times b = abc\)
2.角錐・円錐の表面積と体積
角錐・円錐の表面積と体積
\(① 角錐の表面積=底面積+側面積\)
\(② 円錐の表面積=底面積+(母線を半径とする円の面積)\times \frac{底面の半径 \quad}{母線の長さ \quad}\)
\(③ 角錐・ 円錐の体積=底面積\times 高さ\times \frac{1}{3}\)
展開図をイメージすると分かりやすい。
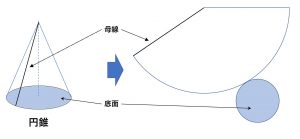
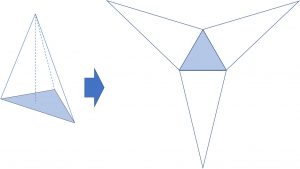
例).下記の円錐の表面積と体積を求める。
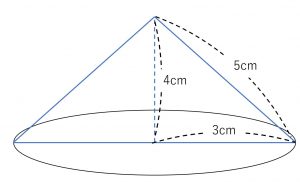
\(円錐の体積 = 3^2\pi\times 4\times \frac{1}{3} = 12(cm^3) \)
3.球の表面積と体積
球の表面積と体積
球の半径を\(r\)とする。
\(球の表面積 = 4\pi r^2 \) \(球の体積 = \large{\frac{4\pi r^3}{3}} \)理解を深める
◆球の表面積
中学生のレベルで分かりやすく説明している動画です。
円の面積の4倍（\(4\times \pi r^2\)）が球の表面積だと分かります。
◆球の体積
下記のように、球の中心\(O\)を頂点とした四角錘を考える。
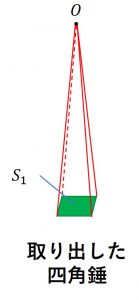
今底面積\(S_1\)の四角錘を図示している。
この四角錘の体積は、球の半径を\(r\)とすると、
\(四角錘の体積 = \frac{1}{3}S_1 r\)となる。球の体積はこの四角錘の体積の合計となるので、
\(\begin{align}球の体積 &= \frac{1}{3}S_1 r + \frac{1}{3}S_2 r + \frac{1}{3}S_3 r + \dots \\ &= \frac{1}{3}r(S_1 + S_2 + S_3 + \dots )\end{align}\)となる事が分かる。この四角錘の底面積の合計は、分割のやり方から球の表面積に等しいことが分かる。
そのため
\(\begin{align}球の体積 &= \frac{1}{3}r(S_1 + S_2 + S_3 + \dots ) \\ &= \frac{1}{3}r\cdot 4\pi r^2 \\ &= \frac{4\pi r^3}{3}\end{align}\)となる。
