相似な図形
1.相似
相似とは
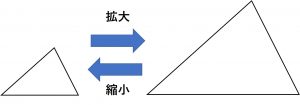
ある図形を形を変えないで拡大または縮小した図形は、元の図形と相似であるという。相似の記号∽。
相似な図形の性質
① 対応する線分の比が等しい。
② 対応する角の大きさが等しい。
2.三角形の相似条件
三角形の合同条件
① 3組の辺の比が全て等しい。
\quad AB:A^{\prime}B^{\prime} = BC:B^{\prime}C^{\prime} = CA:C^{\prime}A^{\prime}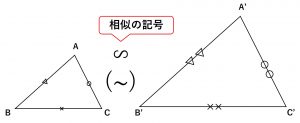
② 2組の辺の比が等しく、その間の角が等しい。
\quad AB:A^{\prime}B^{\prime} = BC:B^{\prime}C^{\prime} \quad \angle B = \angle B^{\prime}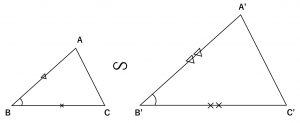
③ 2組の角がそれぞれ等しい。
\quad \angle B = \angle B^{\prime} \quad \angle C = \angle C^{\prime}
3.平行線と線分の比
三角形と比
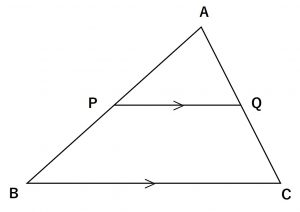
\triangle ABC の辺 AB,AC上にそれぞれP,Qがある時
\begin{align}① PQ // BC ならば,\quad & AP:AB = AQ:AC=PQ:BC \\ & AP:PB = AQ:QC \end{align}
\begin{align}② AP:AB=AQ:AC ならば,PQ // BC \end{align}
\begin{align}③ AP:PB=AQ:QC ならば,PQ // BC \end{align}
平行線と線分の比
3つ以上の平行線に他の2直線が交わる時、対応する線分の比は等しい。
a // b // c のとき、m:n=m^{\prime}:n^{\prime}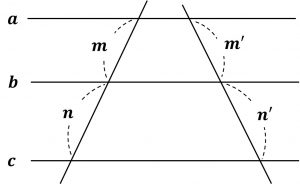
中点連結定理
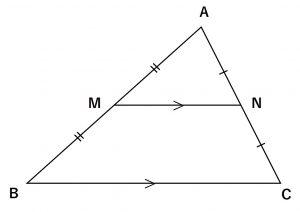
\triangle ABCの辺AB,AC上にそれぞれM,Nがあるとき、
① M,NがそれぞれAB,ACの中点ならば
\quad MN // BC \quad , \quad MN = \frac{1}{2}BC
②Mが辺ABの中点でMN // BC ならば \quad , \quad AN =NC
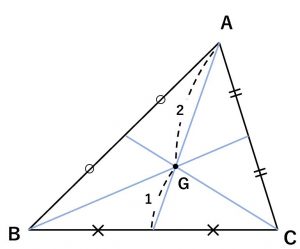
三角形の重心
三角形の1つの頂点と、この頂点に向かい合う辺の中点を結ぶ線分を中線という。
この時、三角形の3つの抽選は1点でGで交わる。
この1点を三角形の重心と言う。
4.相似な図形の面積比・体積比
相似な図形の面積比と体積比
相似な図形の面積比は相似比の2乗に等しく、相似な図形の体積比は相似の3乗に等しい。
相似比 \quad m:n \quad \to \quad 面積比 \quad m^2:n^2 \quad \to \quad 体積比 \quad m^3:n^3