2次関数
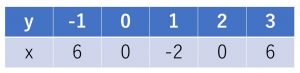
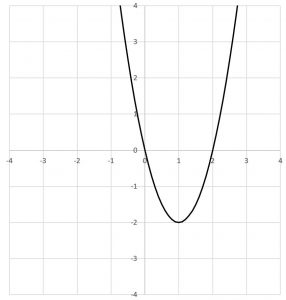
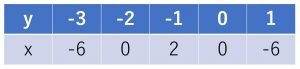
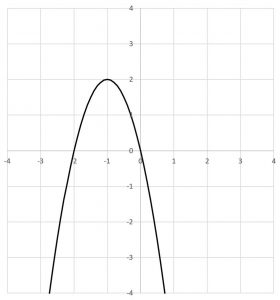
1.2乗に比例する関数
二乗に比例する関数
次数が2の単項式で表される関数。
二乗に比例する関数の特徴
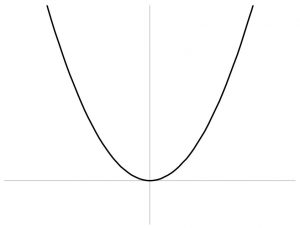
① 原点を頂点として通る。
② y=ax^2と表される時、y軸に線対称の放物線である。
③ 変化の割合が一定ではない。
2.2次関数
二次関数とは
最高次数が2の多項式で表される関数。
y=ax^2+bx+c \quad (a \neq 0)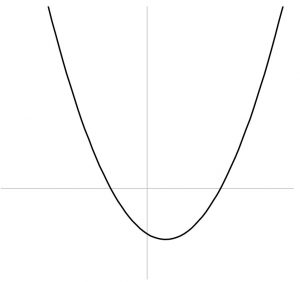
2次関数の特徴
y=ax^2+bx+c \quad (a \neq 0)について
\begin{align}① \quad & a \gt 0 の時、下に凸。 \\ & a \lt 0 の時、上に凸。\\ \end{align} \begin{align}② \quad & a \gt 0 の時、最小値がある。 \\ & a \lt 0 の時、最大値がある。 \end{align}③ 頂点は(x,y)=(-\frac{b}{2a},\frac{4ac-b^2}{4a})。
④ 軸 x=-\frac{b}{2a} に対して線対称。
⑤ y=0の時の二次方程式の解は、x軸と交わる座標。
関連 >> グラフの書き方
①～④について
3.放物線と直線
放物線と直線の交点
放物線(y=ax^2+b)と直線(y=mx+n)の交点を求める。
ax^2+b = mx +n \quadの解が交点のx座標になります。
解をx=p,qとすれば、交点の座標は、
A(p,ap^2+b)とB(q,aq^2+b)である。
何故 = で結ぶのか
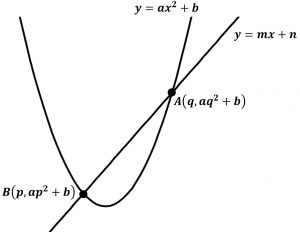
ある二つの曲線や直線の交点を求める際に、=で式を結んで解を求める事が多いです。
その理由を説明していきます。
放物線y=ax^2+bと直線y=mx+nがあります。
仮の交点のx座標をx=p,qとする。
x=pでは、放物線と直線のy座標は同じなので
ap^2+b = mp+n同様にx=qの時も同じで
aq^2+b = mq+nなので、結局のところ
ax^2+b = mx+nを解くのと同じという事がわかる。
