集合
1.集合の表し方
集合 : ある条件をみたすものの集まりの事。集合を表すのに、よくアルファベットの大文字を使います。
要素 : 集合をつくっている「もの」の事。要素を表すのに、よくアルファベットの小文字を使います。
有限集合 : 有限個の要素からなる集合
無限集合 : 無限に多くの要素を含む集合
\(a \in A(A\ni a)\) : aが集合Aの要素であること
\(x \notin A\) : xが集合Aの要素でないこと
集合の要素を書き並べる方法で\(\{ \}\)の中に要素を列挙する。
\(\{ x|p(x) \}\) : \(p(x)はx\)の満たすべき条件で文章、等式、不等式などで表される。
例1).1から10までの自然数を集合Sとすると、
\( S = \{ 1,2,3,4,5,6,7,8,9,10 \} \)である。
\(6 \in S,\quad 9 \in S, \quad 13 \notin S\)と表せる。
例2).\( B = \{x | x=3m+2 , 1 \leq m \leq 5 \} \)
つまり
\(B = \{ 5,8,11,14,17 \}\)
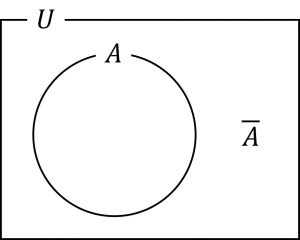
全体集合 : 集合を扱っているとき、そこで扱っている対象の全てのものの集合。\(U\)で表す。
空集合 : 全く要素のない集合。記号\(\emptyset = \{ \}\)と表す。
補集合:\(集合Aに対して、全体集合Uの要素でAに含まれないものの集合を、Aの補集合と言う。\overline{ A }\)で表す。
補集合には次の性質がある。
\((\overline{ \overline{A} }) = A , \quad \overline{U} = \emptyset, \quad \overline{\emptyset} = U\)
2.包合関係
2つの集合A,Bが全く同じ要素を持っている時、AとBとは等しいと言い、\(A=B\)と言う。
部分集合:2つの集合A,Bがあって、Aの要素がすべてBの要素であるとき、すなわち\(a \in A \quad ならば a \in B \quad であるとき、AをB\)の部分集合といい、
\(A \subset B \quad または \quad B \supset A\)と表す。この時AはBに含まれる、またはBはAを含むと言う。
\(A \subset B \quad かつ \quad A\neq B\)のとき、AはBの真部分集合と言う。
\(A \subset B \quad かつ \quad A \supset B \Longleftrightarrow A=B\)となる。
※空集合は全ての集合の部分集合と考えます。
\(\emptyset \subset A\)
3.ベン図
複数の集合の関係や、集合の範囲を図式化したもの。
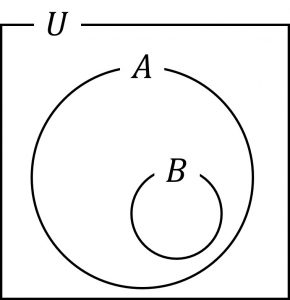
例).部分集合 \(A \subset B \quad かつ \quad A \neq B\)
4.和集合と共通部分
\(A \cup B\):2つの集合A,Bの少なくとも一方に属する要素全体の集合をAとBの和集合、または結びと言います。
\(A \cup B = \{ x | x \in A または x \in B \} \)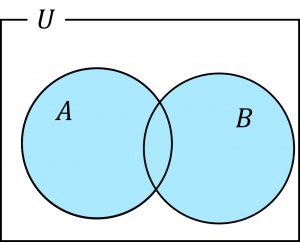
色がついた部分が \(A \cup B\) となる。
\(A \cap B\):2つの集合A,Bの両方に属する要素全体の集合をAとBの共通部分、または交わりと言います。
\(A \cap B = \{ x | x \in A かつ x \in B \} \)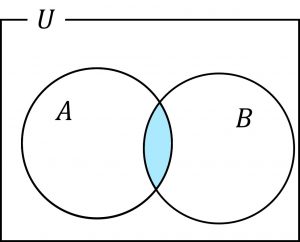
色がついた部分が \(A \cap B\) となる。
和集合(\( A \cup B\))と共通部分(\( A \cap B\))の記号のイメージです。
① \(A \cup B = B \cup A, \quad A \cap B = B\cap A \quad \quad (交換法則)\)
② \(\begin{align} & (A \cup B) \cup C = A\cup (B \cup C) \quad \quad (結合法則) \\ & (A \cap B) \cap C = A\cap (B \cap C)\end{align}\)
③ \(\begin{align} & A\cap (B\cup C) = (A \cap B)\cup (A \cap C) \quad \quad (分配法則)\\ & A\cup (B\cap C) = (A \cup B)\cap (A \cup C) \end{align}\)
④ \(A \cap A = A,\quad A\cup A = A \quad \quad (べき等律)\)
⑤ \(A \cap (A \cup B) = A,\quad A\cup(A\cap B) = A \quad \quad (吸収律)\)
⑥ \(\overline{A\cap B} = \overline{A} \cup \overline{B},\quad \overline{A\cup B} = \overline{A} \cap \overline{B} \quad \quad (ド・モルガンの法則)\)
⑦ \(A \cap U = A,\quad A\cup U = U , \quad A\cap \emptyset = \emptyset , \quad A\cup \emptyset = A\)