立体の表面積と体積
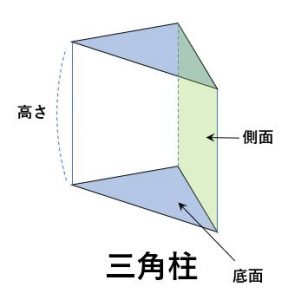
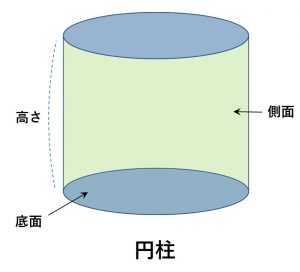
1.角柱・円柱の表面積と体積
角柱・円柱の表面積と体積
底面の面積を底面積。側面全体の面積を側面積と言う。立体全体の表面全体の面積を表面積という。
① 角柱・円柱の表面積=底面積\times2+側面
② 角柱・円柱の表面積=底面の周の長さ\times高さ
③ 角柱・円柱の体積=底面積\times高さ
例).3辺の長さがa,b,cの直方体がある。この直方体の表面積と体積を求める。
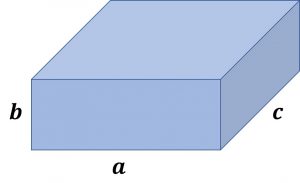
体積=底面積\times 高さ=ac\times b = abc
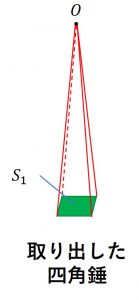
2.角錐・円錐の表面積と体積
角錐・円錐の表面積と体積
① 角錐の表面積=底面積+側面積
② 円錐の表面積=底面積+(母線を半径とする円の面積)\times \frac{底面の半径 \quad}{母線の長さ \quad}
③ 角錐・ 円錐の体積=底面積\times 高さ\times \frac{1}{3}
展開図をイメージすると分かりやすい。
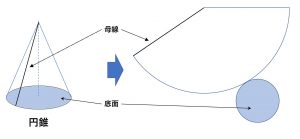
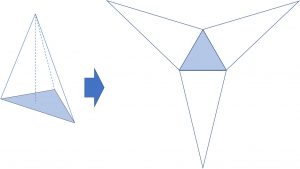
例).下記の円錐の表面積と体積を求める。
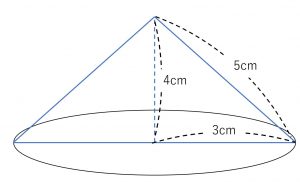
円錐の体積 = 3^2\pi\times 4\times \frac{1}{3} = 12(cm^3)
3.球の表面積と体積
球の表面積と体積
球の半径をrとする。
球の表面積 = 4\pi r^2 球の体積 = \large{\frac{4\pi r^3}{3}}理解を深める