2次不等式
1.2次不等式の解
2次不等式の解
\(\alpha,\betaは実数で\alpha \lt \beta\)とすると
\(y=(x- \alpha)(x-\beta)\)のグラフを用いて
① \((x- \alpha)(x-\beta) \gt 0\) の解は
\(\quad \quad x \lt \alpha,\quad \beta\lt x\)② \((x- \alpha)(x-\beta) \lt 0\)の解は
\(\quad \quad \alpha \lt x \lt \beta\)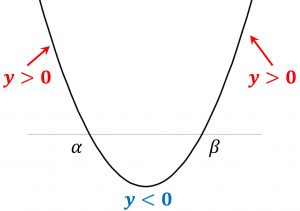
例1).\((x+7)(x-3) \gt 0 \quad の時のx\)の範囲を求める。
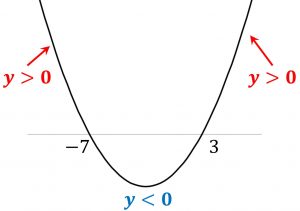
例2).\((x+7)(x-3) \lt 0 \quad の時のx\)の範囲を求める。
\(-7 \lt x \lt <3\)
2.2次不等式の解法
2次方程式 \(ax^2+bx+c = 0\) の実数解は\(\alpha,\beta \quad (\alpha \lt \beta)\) とする。
\(a \gt 0 \)の時、
| Dの符号 | \(D \gt 0\) | \(D = 0\) | \(D \lt 0\) |
| \(y=ax^2+bx+c\)のグラフ |  |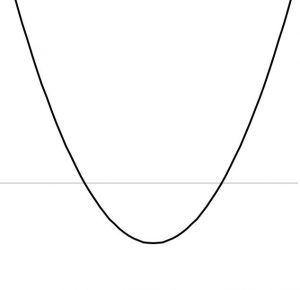
 |
 |
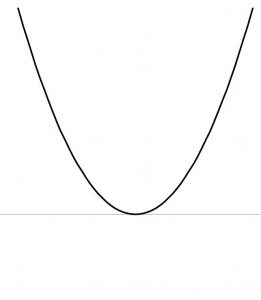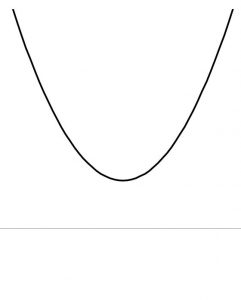| \(ax^2+bx+c \gt 0\)の解 | \(x \lt \alpha , \beta \lt x\) | \(\alpha\)以外の実数全体 | 実数全体 |
| \(ax^2+bx+c \geq 0\) | \(x \leq \alpha , \beta \leq x\) | 実数全体 | 実数全体 |
| \(ax^2+bx+c \lt 0\) | \(\alpha \lt x \lt \beta\) | 解なし | 解なし |
| \(ax^2+bx+c \leq 0\) | \(\alpha \leq x \leq \beta\) | \(x= \alpha\) | 解なし |
3.連立不等式
連立不等式の解
2つ以上の不等式を同時に満足する解を連立不等式の解。
例).\(\begin{cases} x^2-8x+10 & \gt 0 \dots ① \\ x^2-8x-12 & \lt 0 \dots ② \end{cases}\)を解く。
①より\((x-2)(x-5) \gt 0 \quad \to \quad x\lt 2,\quad 5\lt x\)
①より\(\{ x-(4-2\sqrt{7}) \} \{ x-(4+2\sqrt{7}) \} \lt 0 \quad \to \quad 4-2\sqrt{7} \lt x \lt 4+2\sqrt{7}\)
よって
\(4-2\sqrt{7} \lt x \lt 2 , \quad 5\lt x \lt 4+2\sqrt{7}\)
4.関連
関連 >> 2次不等式・基本問題1
