三角形の定理や性質
1.三平方の定理（ピタゴラスの定理）
三平方の定理
別名：ピタゴラスの定理
三角形において、成り立つ公式です。
\angle C = 90^{\circ} \Longleftrightarrow a^2+b^2 = c^2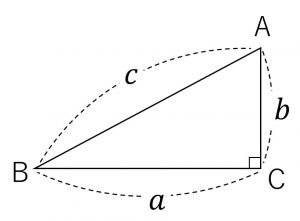
角と辺の関係
\triangle ABCで \angle A , \angle B , \angle C の対辺の長さを,それぞれa,b,cとするとき、次の事が成り立つ。
\angle C \lt 90^{\circ} \to a^2+b^2 \lt c^2 \angle C = 90^{\circ} \to a^2+b^2 = c^2 \angle C \gt 90^{\circ} \to a^2+b^2 \gt c^2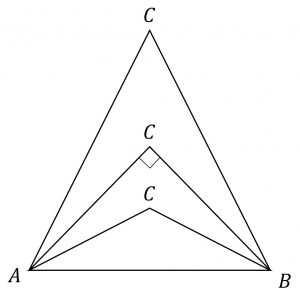
2.三角形の中線と垂線
中線定理（パップスの定理）
\triangle ABC のBCの中点をMとすれば
AB^2 + AC^2 = 2(AM^2+BM^2)
垂線の性質
AH \perp BC , BCの中点をMとすれば
AB^2-AC^2 = BH^2-CH^2 = 2BC \cdot MH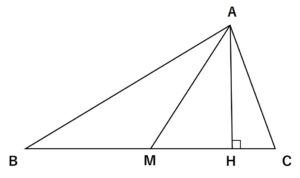
3.内分点と外分点
内分点
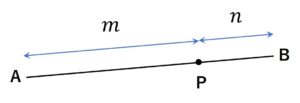
・線分AB上にある点。
・線分AB上をm:nに内分する点Pは、AP:BP=m:nの関係性にある。
外分点
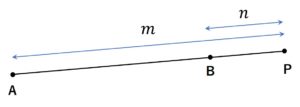
・線分AB上にない直線AB上の点。
・線分ABをm:nに外分する点Pは、AP:BP=m:nの関係性にある。
三角形の角の2等分線と比例
三角形の内角、外角の二等分線での内分点、外分点の関係性
\triangle ABCで\angle Aおよびその外角の二等分線が直線AB上に交わる点をM、Nとすると
AB:AC = BM:MC=BN:NCとなり、逆も成り立つ。
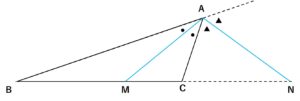
また上の式が成り立つとき、
M、NはBCを調和に分けるといい、
B、M、C、Nを調和点列という。
4.三角形と直線
メネラウスの定理
\triangle ABCを1つの直線で切り、
辺BC、CA、ABまたはその延長との交点をD、E、Fとすれば
\large{\frac{BD}{DC}\cdot \frac{CE}{EA} \cdot \frac{AF}{FB}=1}
逆も成り立つ。
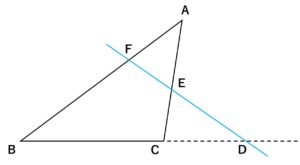
※覚え方
三角形を作るように、点を辿っていけば分かりやすい。
\large{\frac{BD}{DC}\cdot \frac{CE}{EA} \cdot \frac{AF}{FB}=1}について
B \to D \to C \to E \to A \to F \to B例題
下記の図でAM:MB=2:1、\quad AN:NC=3:2、BNとCNとの交点をPとする。
BP:PNを求めよ。
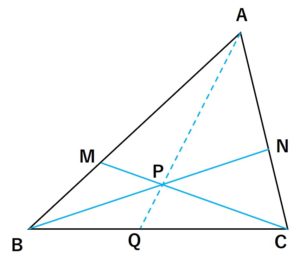
解答).\triangle ABN に注目して、直線MPNで切ると、メネラウスの定理より
\begin{align} \frac{BP}{PN}\cdot\frac{NC}{CA}\cdot\frac{AM}{MB} &= 1 \\ \frac{BP}{PN}\cdot\frac{2}{5}\cdot\frac{2}{1} &= 1 \\ \frac{BP}{PN} &= \frac{5}{4} \end{align}よって
BP:PN=5:4
チェバの定理
\triangle ABC の平面上に1点Oをとり、
AO、BO、COと大変またはその延長との交点をD、E、Fとすれば
\large{\frac{BD}{DC}\cdot \frac{CE}{EA} \cdot \frac{AF}{FB}=1}となる。逆も成り立つ。
例題
下記の図でAM:MB=2:1、\quad AN:NC=3:2、BNとCNとの交点をPとし、直線APと線分BCとの交点をQとする。
BQ:QCを求めよ。
解答).\(\triangle ABC に対して、チェバの定理より
[latex]\begin{align} \frac{BQ}{QC}\cdot\frac{CN}{NA}\cdot\frac{AM}{MB} &= 1 \\ \frac{BQ}{QC}\cdot\frac{2}{3}\cdot\frac{2}{1} &= 1 \\ \frac{BQ}{QC} &= \frac{3}{4} \end{align}\)よって
BQ:QC=3:4
