連立方程式の解法 1
1.連立1次方程式 1
(1)、(2)で1つの未知数を消去して1元1次方程式を導く。
消去の方法には、加減法、代入法、等値法がある。
① \(a_1b_2-a_2b_1 \neq 0\) の時、
\(x=\frac{c_1b_2-c_2b_1}{a_1b_2-a_2b_1},\quad y=\frac{a_1c_2-a_2c_1}{a_1b_2-a_2b_1}\)
② \(a_1b_2-a_2b_1 = 0\) の時、
(\(\alpha\)) \(\frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2}\)
ならば、解は無数に存在する。グラフを描けば、直線が重なる状態。
(\(\beta\)) \(\frac{a_1}{a_2} = \frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)
ならば、解は存在しない。グラフを描けば、直線が平行になる状態。
を解け。
解答).
(加減法) \(①\times2+②\times3\)より
\(\begin{cases} 10x-6y-26 &=0 \quad \cdots ①’\\ 9x+6y-12 &= 0 \quad \cdots ②’ \end{cases}\)\(\quad \Longrightarrow 19x = 38 \quad (∴ x=2)\)
このxの解を①、もしくは②に代入してyを求めると
\(∴y=-1\)となる。
\(\begin{cases} x=2 \\ y=-1 \end{cases}\)
(1) \(
\begin{cases} A=B \quad \cdots ①\\ C=D \quad \cdots ② \end{cases}
\quad \Longleftrightarrow \quad
\begin{cases} A=B \quad \cdots ③ \\ lA+mC = lB +mD \quad (m \neq 0) \cdots ④ \end{cases}
\)
この関係は
①②が分かれば(\(\Longrightarrow\))、③④が加減法で作れる、
③④が分かれば(\(\Longleftarrow\))、①②が加減法で作れる、
という関係にあります。
(2) \(
\begin{cases} y=f(x) \\ g(x,y)=0 \end{cases}
\quad \Longleftrightarrow \quad
\begin{cases} y=f(x) \\ g(x,f(x))=0 \end{cases}
\)
これは代入法による同値関係です。
\begin{cases} y=k(x-x^3) \quad \cdots ① \quad x \gt 0 \\ x=k(y-y^3) \quad \cdots ② \quad y \gt 0 \end{cases}
\quad x \neq y\)
の式を満たす\(k\)の条件を求めよ。
解答).
まず初めにk=0の時、式は成り立たないので、\(k \neq 0\)
①-②、①+②より
\(\begin{cases} y-x=k\{ (x-y) – (x^3-y^3) \} \quad \cdots ③ \\ y+x=k\{ (x+y) – (x^3+y^3) \} \quad \cdots ④ \end{cases}\)
③、④より、①、②が加減法で作れるので、同値関係となる。
つまりこの式を満たすkの条件を満たせば、題意を示せたと言える。
③、④を変形して
\(\Longrightarrow \begin{cases} k(x-y)\{ 1 – (x^2+xy+y^2) + \frac{1}{k} \}=0 \quad \cdots ③ \\ k(x+y)\{ 1 – (x^2-xy+y^2) – \frac{1}{k} \}=0 \quad \cdots ④ \end{cases}\)
\(k \neq 0 ,\quad x \gt 0, \quad y \gt 0 ,\quad x\neq y\)より、
\(\Longrightarrow \begin{cases} 1 – (x^2+xy+y^2) + \frac{1}{k} =0 \quad \cdots ③’ \\ 1 – (x^2-xy+y^2) – \frac{1}{k} =0 \quad \cdots ④’ \end{cases}\) \(
\Longrightarrow \begin{cases} x^2+y^2+xy =1+ \frac{1}{k} \quad \cdots ③’ \\ x^2+y^2-xy = 1- \frac{1}{k} \quad \cdots ④’ \end{cases}\)
同値関係から
\(\Longrightarrow \begin{cases} x^2+y^2=1 \quad \cdots ⑤ \\ xy = \frac{1}{k} \quad \cdots ⑥ \end{cases}\)
を満たせばよい。
⑤は円の式、⑥は反比例の式となり、これをグラフに表すと、
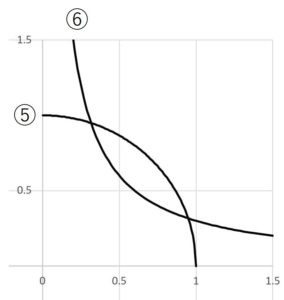
となる。
この2曲線が交わる時に解が存在する。
\(k=\frac{1}{2}\)の時

となり、\((x,y)=(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})\)が解となる。
例題の範囲を満たさない。
よって、\(0 \lt k \lt \frac{1}{2}\)
\(x,y,z\)のうち1つを消去して2元連立1次方程式を導いて解く。
a_1x+b_1y+c_1z=0 \\
a_2x+b_2y+c_2z=0
\end{cases} \\
(a_1:b_1:c_1 \neq a_2:b_2:c_2)
\)
から、\(x:y:z\)が定まり
\(\large{ \frac{x}{b_1c_2 -b_2c_1} = \frac{y}{c_1a_2 -c_2a_1} = \frac{z}{a_1b_2 -a_2b_1} }\)

