円に関する定理や性質
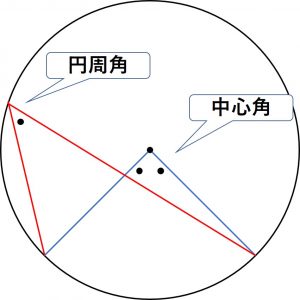
1.円周角の定理
円周角の定理
円の性質。
① 同じ弧に対する円周角は全て等しい。
② 円周角は中心角の半分である。
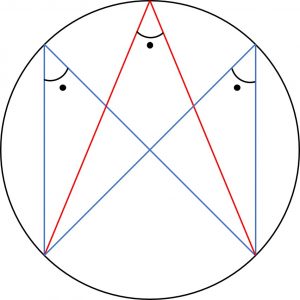
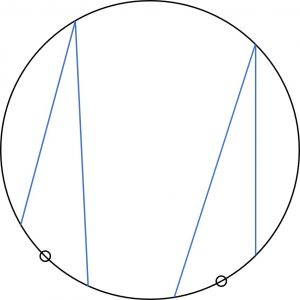
円周角と弧
円の性質。
① 弧が等しい ⇔ 円周角が等しい
② 弧の長さは円周角の大きさに比例する。
円に内接する四角形
円に内接する四角形の性質
① 1組の向かい合う内角の和が180^{\circ}である。
\quad \quad \angle BAD + \angle BCD = 180^{\circ}、\quad \angle ABC + \angle CDA = 180^{\circ}② トレミーの定理
\quad \quad AB\cdot CD + BC \cdot DA = AC \cdot BD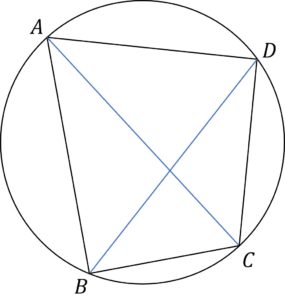
円に外接する四角形
四角形ABCDが円に外接する時、下の式が成り立つ。
\quad \quad AB+CD = BC+DA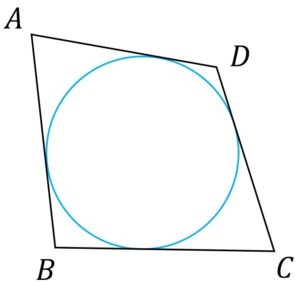
2.円と線
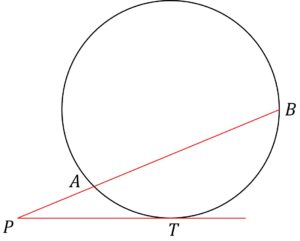
接線と弦との角
接線ALと弦ABにおいて
\angle BAT = \angle APB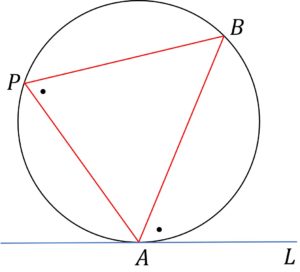
2円の弦
2円O、O^{\prime}が2点A、Bで交わるとき
Aを取る
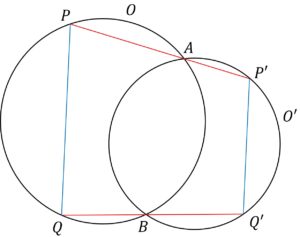
3.円と比例
方べきの定理
① 2弦AB、CDが点Pで交わる時
\quad \quad PA \cdot PB = PC \cdot PD逆も成り立つ
② この時、円の半径をrとすると
\quad \quad PA \cdot PB = | r^2 -OP^2 |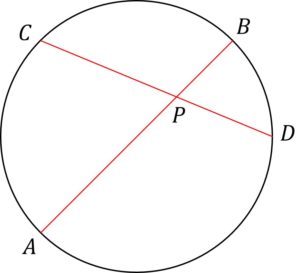
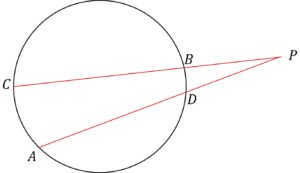
接線の定理
円外の点Pからひいた接線をPT、割線をPABとすると、
\quad \quad PT^2 = PA \cdot PB