順列と組合せ
1.場合の数
ある事柄において、起こりうる全ての場合の数の総数を、場合の数と言う。
2つの事柄A,Bが同時に起こらない時、Aの起こる場合の数がm通り、Bの起こる場合の数をn通りの時
AまたはBのどちらかが起こる場合の数は、\((m+n)通り\)
例1).区別がつく、りんごが3個、みかんが4個ある。この中からどれか1つを選ぶ方法は何通りありますか。
今この中からどれか1つを選ぶ方法は、りんごが3通り、みかんが4通りある。
そのため、和の法則より、3+4=7通り
2つの事柄A,Bがあって、Aの起こる場合の数がm通り、それに対して、Bの起こる場合の数がn通りある時
A、Bが同時に起こる場合の数は、\((m\times n)通り\)
例2).サイコロを2回振ります。1回目の出目をA、2回目の出目をBとする。A,Bの出目の場合の数は何通りありますか。
Aは6通り、Bは6通りあるので、\(6\times 6 = 36通り\)
物事を順番に書き出し、場合の数を数えるテクニックです。
例3).裏表のあるコインがあり、2回コイントスをします。1回目の結果をA、2回目の結果をBとするときの場合の数は何通りありますか。
この時の樹形図は
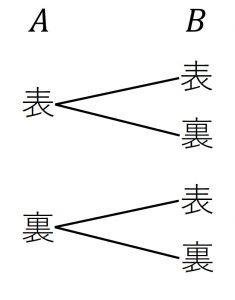
となる。
そのため、場合の数は4通り。
2.順列
いくつかのものを並べる時、順番に並べる並べ方を順列と言う。
一般に、異なるn個のものからr子取り出し、順番に並べる並べ方は、
\({}_n \mathrm{ P }_r = n\times (n-1)\times \dots (n-(r-1))\)特に\(n=r\)の時
\({}_n \mathrm{ P }_n =n! = n\times (n-1) \times \dots \times 2 \times 1 \)となります。
\(n!\)はnの階乗と言います。
例1).7人の生徒から3人を選び、順番に並べる並べ方は、
\(7\times 6 \times 5 = 210\)通り
異なるn個のものから、同じものを繰り返して取ることを許して、r個とる順列の数を\({}_n \Pi_r\)と表す。
\({}_n \Pi_r = n^r\)例2).5個のさいころを同時に投げる時、目の積が奇数となる場合の数を求めよ。
各々のさいころについて、1,3,5の3通りの奇数が出ればよいので、
\({}_3 \Pi_5 = 3^5 = 243 (通り)\)
・異なるn個のものを円形に並べる並べ方の数は、 \((n-1)!\)
・異なるn個のものからr個取って、円形に並べる並べ方は\( {}_n C_r \cdot (r-1)!\)
※\({}_n C_r\)については次章で説明。
3.組合せ
並べ方を考えないで、メンバーだけを区別して選ぶ選び方を組合せと言う。
一般に異なるn個のものからr個選ぶ選び方は、
\({}_n \mathrm{ C }_r = \large{\frac{n\times (n-1) \times \dots (n-(r-1))}{r\times (r-1) \times (r-2) \times \dots 2 \times 1} } = \large{\frac{{}_n \mathrm{ P }_r}{r !}}\)となります。
① \({}_n C_c = 1,\quad {}_nC_1 = n \quad ({}_n C_0 = 1 と定める)\)
② \({}_n C_{n-r} = {}_n C_{r} \)
③ \({}_n C_{r} = {}_{n-1} C_{r-1} + {}_{n-1} C_r\)
例1).7人の生徒から3人を選ぶ方法は、
\(\frac{7\times 6 \times 5}{3\times 2\times 1} = 35\)通り
n個の要素から出来ている集合を、a個、b個、c個\((a+b+c=n)\)の3つの組に分割する方法は
\({}_n C_a \times {}_{n-a} C_b \quad (通り)\)例2).9人を2人、3人、4人に分ける方法の数を求める。
\({}_9 C_2 \times {}_7 C_3 = \frac{9\cdot 8}{2\cdot1}\cdot\frac{7\cdot 6 \cdot 5}{3 \cdot 2 \cdot 1}=1260 (通り)\)