正の数、負の数
1.数字の種類
0より大きい数。
(例:2 ,23 ,1.3 , 2/5)
0より小さい数。
(例:-3, -42, -2.9, -6/11)
0および、0から次々に1を足した数、もしくは次々に1を引いた数。
(例:-12, -4, 0, 6, 15)
正の整数
(例:6, 15 ,57)
正の数に符号をつけるなら+(読み方:プラス)。
負の数には符号―(読み方:マイナス)をつける。
2.絶対値と数直線
- 絶対値・・・ 数直線上で、0からの距離。
例).23の絶対値は23。-14の絶対値は14。これを記号で表すと、
|23|=23 |-14|=14

3.加法と減法
- 同符号の2数の和・・・絶対値の和に、共通の符号をつける。
(+2)+(+5)=+7=7
(-3)+(-2)=-5
- 異符号の和・・・絶対値の差に、絶対値の大きいほうの符号をつける。
(-4)+(+7)=+(7-4)=+3
(-5)+(+3)=-(5-3)=-2
- 減法・・・ひく数の符号を変えて加える。
(-4)-(+2)=(-4)+(-2)=-6
(-4)-(-2)=(-4)+(+2)=-2
- 加減の混じった計算・・ひく数の符号を変えて加法に直し、同じ符号の数をまとめる。
(+3)+(-2)-(+4)-(-1)=(+3)+ (-2)+(-4)+(+1)
=(+4)+(-6)=(-2)
4.乗法と除法
1. 同符号の2数の積
(+2)×(+3) = +(2×3) = 6 (小学校と同じ)
2. 異符号の2数の積
(-2)×(+3) = -(2×3) = -6
5.逆数
その数とかけると1になる数を、他方の数の逆数という。
例1).2 の逆数は \frac{1}{2}
例2).\frac{2}{3} の逆数は \frac{3}{2}
例3). -2 の逆数は -\frac{1}{2}
分数を含む除法では、割る数の逆数を掛けて、掛け算(乗法)で計算する。
例1). 2 \div 2 = 2 \times \frac{1}{2} = 1
例2). \frac{3}{4} \div \frac{1}{2} = \frac{3}{4} \times \frac{2}{1} = \frac{3}{2}
例3). 2 \div (-2) = 2 \times (-\frac{1}{2}) = -1
6.分配法則
次のような計算が成り立つ、数学の法則の事。
・ 〇 \times (△ + □) = 〇 \times △ + 〇 \times □
・ (△ + □) \times 〇 = △ \times 〇 + □ \times 〇
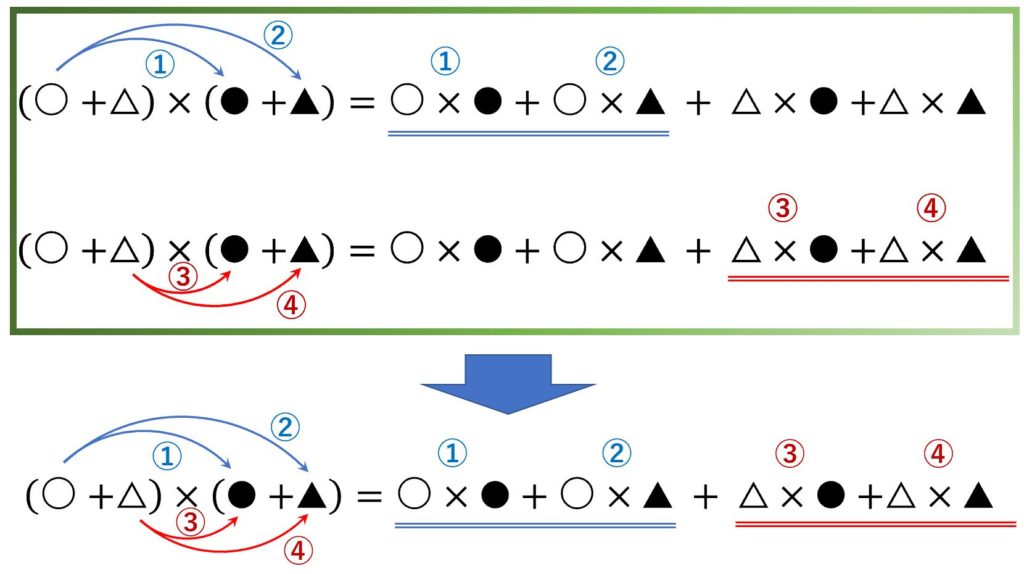
・ (〇+△) \times (● + ▲) = 〇 \times ● + 〇 \times ▲ + △ \times ● + △ \times ▲
例1). 2 \times (1+5) = 2\times 1 + 2\times 5 = 2 + 10 = 12
例2). (2+3) \times 4 = 2\times 4 + 3 \times 4 = 8 + 12 = 20
例3). (2+3) \times (4+5) = 2\times 4 + 2\times 5 + 3\times 4 + 3\times 5
= 8 +10 +12 +15 = 45
例4). (3+4)\times (5-6) = 3\times 5 + 3\times (-6) + 4\times 5 + 4\times (-6)
= 14 -18 +20 -24 = -7
関連 >> 【問】負の数