2次関数のグラフと移動
1.関数記号
関数とは
ある二つの変数x,yがあり、xの各値に対応してyの値がただ1つに定まる時、yはxの関数であるという。
例).\(y=2x+1\)
定義域・値域とは
変数xの関数に置いて、変数xの取り得る値の範囲をxの変域（定義域）
定まる変数yの値の範囲を、yの値域
という。
関数記号とは
yがxの関数であることを\(y=f(x),y=g(x)\)などの記号で表す。
また\(x=a\)における関数の値を\(f(a)\)と表す。
2.2次関数のグラフ
\(y=a(x-p)^2+q \quad (a \neq 0)\)
このように平方完成する事によって、グラフの概要を知る事が出来る。
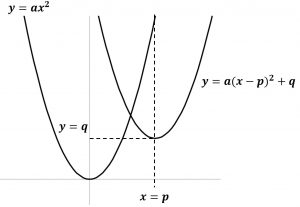
① \(y=ax^2\)のグラフをx軸にp,y軸方向にqだけ平行移動した放物線。
② 頂点：(\(p,q\))、 軸：\(x=p\)
\(y=f(x)\)のグラフの移動
① \(x軸方向にa,y軸方向にbだけ平行移動すると\)
\(y-b=f(x-a)\)のグラフとなる
② 対称移動
\(x軸対称 \dots y=-f(x)\) \(y軸対称 \dots y=f(-x)\) \(原点対称 \dots y = -f(-x)\)※2次関数でなくても成り立つ。
例1).関数 \(y= -2x^2+ 3x + 3 \quad をx軸方向に2,y軸方向に-1だけ平行移動する。\)
\(\begin{align} y-(-1) &= -2(x-2)^2+3(x-2)+3 \\ y &= -2x^2+9x-12 \end{align}\)例2).関数 \(y=x^2 をy軸\)に対して対称移動する。
\(y = (-x)^2 = x^2\)例3).関数 \(y=x^2 をx軸\)に対して対称移動する。
\(\begin{align} -y &= x^2 \\ y &= -x^2 \end{align}\)
3.関連
関連 >> 2次関数・基本問題1
