2次方程式と因数分解
1.複2次式の因数分解
ax^4+bx^2+c = 0 \quad (a \neq 0)を解く方法2種です。
① x^2=tと置いて、at^2+bt+c = 0の因数分解を用いる。
② ax^4+bx^2+c = a (x^2+p)^2-qx^2 = 0のように平方の差の形にしてみる。
※①に関しては、慣れたら置かなくても出来るようにしましょう。
例1).x^4+5x^2-6 = 0 を解く。
x^2 = t と置く。
\begin{align} t^2+5t-6 &= (t+6)(t-1) \\ &= (x^2+6)(x^2-1) \\ &= (x^2+6)(x+1)(x-1) \\ &=0 \end{align}x = \pm \sqrt{6},\pm1
例2).x^4+2x^2+9 = 0 を因数分解する。
\begin{align} x^4+2x^2+9 &= (x^2+3)^2 -4x^2 \\ &= (x^2+2x+3)(x^2-2x+3) \end{align}
2.判別式と因数分解とグラフ
関連リンク >> 2次方程式
判別式Dと解の個数の関係のおさらい。
ax^2+bx+c=0の式について、
D=b^2-4ac \quad \begin{cases} \gt 0 \quad \text{解の個数は2個} \\ = 0 \quad \text{解の個数は1個} \\ \lt 0 \quad \text{解の個数は0個} \end{cases}
※二次方程式について
① D \lt 0の時、実数解はないので、因数分解は出来ない。
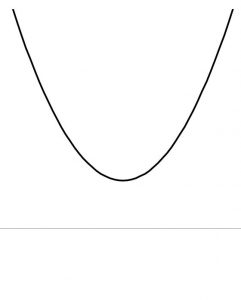
② D = 0の時、重解となり(x-p)^2と因数分解できる。
x軸と接しているx座標が解pとなる。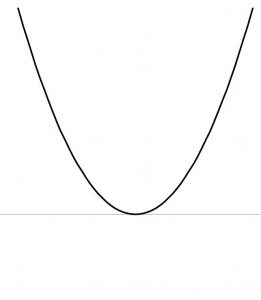
③ D > 0の時、解が二つ出来るので(x-p)(x-q)と因数分解できる。
x軸と交わっているx座標が解p,qとなる。