命題と証明
1.命題と集合
命題「\(p \to q\)」について
・条件\(p\)の要素全体の集合をP
・条件\(q\)の要素全体の集合をQ
とする時、
命題「\(p \to q\)」が真 \(\quad \Longleftrightarrow \quad P \subset Q\)
命題「\(p \Longleftrightarrow q\)」が真 \(\quad \Longleftrightarrow \quad P = Q\)
2.逆,裏,対偶
命題「\(p \to q\)」に対して
\( \quad 「q \to p」を\quad 「p \to q」の逆\) \( \quad 「\overline{p} \to \overline{q}」を\quad 「p \to q」の裏\) \( \quad 「\overline{q} \to \overline{p}」を\quad 「p \to q」の対偶\)と言う。
これらの関係は下記に記してある図の通りである。
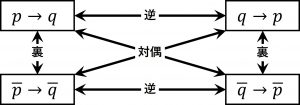
もとの命題が真であっても、その逆と裏は必ずしも真ではない。
例1).\(x \gt 5 \quad ならば \quad x \gt -1\)は真
逆:\(x \gt -1\quad ならば \quad x \gt 5\) は偽
裏:\(x \leq 5\quad ならば \quad x \leq -1\) は偽
命題の真偽で、その命題と対偶の真偽は一致する。
① \(「p \to qが真」 \Longleftrightarrow 「\overline{q} \to \overline{p}が真」\)
② \(「p \to qが偽」 \Longleftrightarrow 「\overline{q} \to \overline{p}が偽」\)
これについては、ベン図を用いれば分かりやすい。
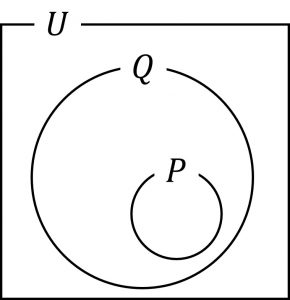
例2).\(x \gt 5 \quad ならば \quad x \gt -1\)は真
対偶:\(x \leq -1\quad ならば \quad x \leq 5\) は真
3.命題と証明
命題「\(p \to q\)」が真である事を、法則や性質を用いて導くことを証明という。
「\(p \to q \quad かつ \quad x\to p \quad ならば \quad x \to q\)」という形式の論法です。
- 背理法
\(p \to q\)を証明するのに「\(p かつ \overline{q}\)」が成り立たない事を示すことで、 「\(p \to q\)」が真であるとする証明法。 - 対偶法
命題と、命題の対偶の真偽が等しいことを使う証明法。「\(\overline{q} \to \overline{p}\)」が真であることを示して、「\(p \to q\)」が真であることを示す。 - 転換法
いくつかの真である命題\(p_1 \to q_1 , \quad p_2 \to q_2 , \quad p_3 \to q_3 , \dots \)があり、家庭が全ての場合を満たし、結論が二つ同時に成立しない時は、各命題の逆\(q_1 \to p_1, \quad q_2 \to p_2, \quad q_3 \to p_3, \dots \)もまた真となる。この方法を転換法という。
例3).(三段論法)「私は人間である。」「人間は哺乳類である。」
この事から、「私は哺乳類である。」
例4).(背理法)A君はCさんの事が「好き」、もしくは「好きではない」のどちらかとする。
A君:「AってCさんの事好きだろ?」
B君:「いや、そ、そ、そんなことないよ」
A君:「なるほど、じゃあCさんの事やっぱり嫌いなんだな?」(背理法の仮定)
B君:「き、嫌いじゃないよ!」(矛盾)
A君:「ってことは、好きなんだろ?」(結論)
例5).(背理法)「\(\sqrt{2}\)は無理数である」事の証明をする。
「\(\sqrt{2}\)は有理数である」と仮定する。
\(\sqrt{2}=\frac{p}{q}\)と表すことが出来る。(\(p,q\)は互いに素な有理数。)
\(2q^2 = p^2となる。\)あとは次の論理となる。
\(2q^2は偶数 \quad \to \quad p^2は2の倍数 \quad \to \quad pは2の倍数 \quad \to \quad p^2は4の倍数 \quad \to \quad q^2は2の倍数 \)となり、\(p,q\)が互いに素である事に矛盾します。
そのため「\(\sqrt{2}\)は無理数である」と言える。
例5).(転換法)「\(2次方程式 ax^2 + bx +c = 0 でD=b^2 -4ac\)」とすると、
\(\begin{align} & D \gt 0 ならば異なる2つの実数解を持つ \\ & D = 0 ならば重解を持つ \\ & D \lt 0 ならば実数解を持たない\end{align}\)
の各命題は真である。
仮定は全ての場合をつくし、結論はどの二つも同時に成り立つことはないので、転換法により逆は全て成り立つ。すなわち
\(\begin{align} & 異なる2つの実数解を持つ ならば D \gt 0 \\ & 重解を持つ ならばD = 0 \\ & 実数解を持たないならばD \lt 0\end{align}\)
が成り立つ。
自然数についての命題の証明に用いる。
※よく数列(数学Bの範囲)の証明に用いられる。
