ロルの定理
1.ロルの定理 (Rolle’s theorem)
有界な閉区間 \( [a,b] \) 上で定理された
連続関数 \( f \) が 開区間 \( (a,b) \) で微分可能であり、
\( f(a) = f(b) \)
を満たすとき、導関数 \( f'(x) \) は
\( f'(c) = 0 \quad (a < c < b) \)
となる \( c \) が少なくとも1つ存在する。
※端の \( a,b \) については微分不可能でもよい。
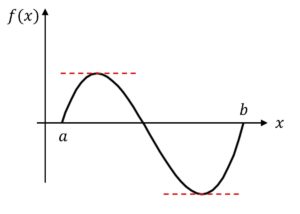
直感的には、\(a < c < b\) 内に少なくとも1つは、\(f'(c) = 0\) となる地点が存在する。
つまり、傾きが0となる地点が存在する。
ちなみにロルの定理を使った問題は、下記の問題しか思いつきません(;^ω^)
ただ、テイラー展開の証明やロピタルの定理の証明などに使われるので、知っておくことは重要です。
\( f(x) \) が \( [a,b] \) で連続で第二次導関数が存在する時、
\[ f(b) = f(a) + f'(a)(b-a) + \frac{1}{2} f”(c)(b-a)^2 \quad (a < c < b)\]
を満たす、\( c \) が少なくとも1つ存在する事を示せ。
例題).
\[ F(x) = f(x) + f'(x)(b-x) + \frac{1}{2}k (b-x)^2 \]
と置く。\(f(x)\) が \( [a,b] \) で第二次導関数があるので、
\( F(x) \) も \( [a,b] \) で第二次導関数が存在する。
この時の \( k \) は \( F(a) = F(b) \) が成立する \( k \) とする
つまり、
\[ f(a) + f'(a)(b-a) + \frac{1}{2}k (b-a)^2 = f(b) \]
となる。
ここで、\( F(x) \) を微分すると
\[ F'(x) = f”(x)(b-x) -k (b-x) \]
ロルの定理より、\( F'(c) = 0 \) となる \( c \quad ( a < c < b ) \) が存在するので、
\( 0 = f”(c)(b-c) – k(b-c) \quad \quad ∴k=f”(c) \)
よって、題意は示せた。
2.ロルの定理の証明 (厳密ではない)
厳密に証明するためには、「最大値・最小値の原理」を証明しなければならないが、ここでは省略する。
いつか記事に書きます。
連続な関数 \( f \) は閉区間 \( [a,b] \) において、必ず最大値・最小値を持つ。
※ この証明には、Bolzano-Weierstrass の定理を用いる。
※現条件 (仮定)
・有界閉区間 \( [ a,b ] \) 上で定義された関数 \( f(x) \)
・関数 \( f(x) \) は連続関数 ( \( [a,b] \) の範囲 )
・関数 \( f(x) \) は \( (a,b) \) で微分可能。
・\( f(a) = f(b) \)。
① \( f(x) = f(a) = f(b) \) となる定数関数の場合
ただし、\( a < x < b \) となる \( x \) とする。
微分の定義式から、
\( (a,b) \) の区間で \( f'(x) = 0 \) となる。
② \( f(x) > f(a) \) であるような関数 \( f(x) \) の場合
ただし、\( a < x < b \) となる \( x \) とする。
\( f(x) \) は区間 \( [a,b] \) で連続であるから、
「最大値・最小値の原理」より、この区間で \( f(x) \) は最大値・最小値を取る。
\( f(a) = f(b) \) より、区間 \( [a,b] \) で \( f(x) \) は
最大値・最小値のうち、少なくとも 1 つは \( f(a) = f(b) \) とは異なる。
つまり、\( ( a,b ) \) で \( f(x) \) は少なくとも 1 つは最大値・最小値を持つ。
ここで、\( f(c) \) が最大値であるとする。
ただし、\( a < c < b \) 、\( f(c) > f(a) \) とする。
次に \( h \) は \( c-a,\quad b-c \) よりも小さい正の数とすると、
\( a < c-h < c+h < b \)
となる。
\( f(c) \) は最大値なので、
\( f(c \pm h) – f(c) \le 0 \)
\[ \frac{f(c-h) – f(c)}{-h} \ge 0,\quad \frac{f(c+h) – f(c)}{h} \le 0 \]
\( f(x) \) は \( x=c \) で微分可能なので、\( h \to +0 \) とすると
\( f'(c) \ge 0 \quad かつ \quad f'(c) \le 0 \)
となるので、
\[ ∴ \quad f'(c) = 0 \]
とする。
③ \( f(x) < f(a) \) であるような \( f(x) \) の場合
②世同様に証明できる。
① ~ ③より、
ロルの定理を証明できた。
