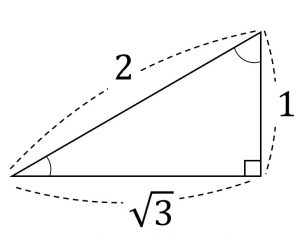
三平方の定理 （ピタゴラスの定理）
1.三平方の定理（ピタゴラスの定理）
三平方の定理
別名：ピタゴラスの定理
三角形において、成り立つ公式です。
\(\angle C = 90^{\circ} \Longleftrightarrow a^2+b^2 = c^2\)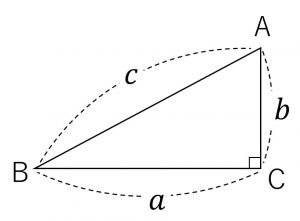
角と辺の関係
\(\triangle ABCで \angle A , \angle B , \angle C の対辺の長さを,それぞれa,b,c\)とするとき、次の事が成り立つ。
\(\angle C \lt 90^{\circ} \to a^2+b^2 \lt c^2\) \(\angle C = 90^{\circ} \to a^2+b^2 = c^2\) \(\angle C \gt 90^{\circ} \to a^2+b^2 \gt c^2\)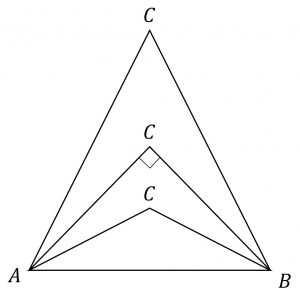
2.三平方尾の定理の証明
よくある証明
下図のような正方形内に、直角三角形が4つ、角に合わせて入っているものを考える。
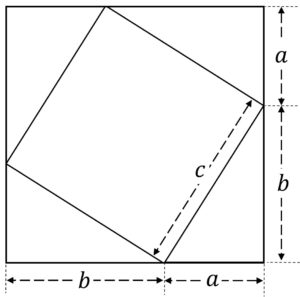
この4つの三角形は、長さ \( a \) と \( b \) の間の角が \( 90^{\circ} \) の直角三角形となっている。
中の四角形は、全ての長さが直角三角形の斜辺の長さ \( c \) となる正方形である。
これらの図形の面積を二方向で見ると下図のようになる。
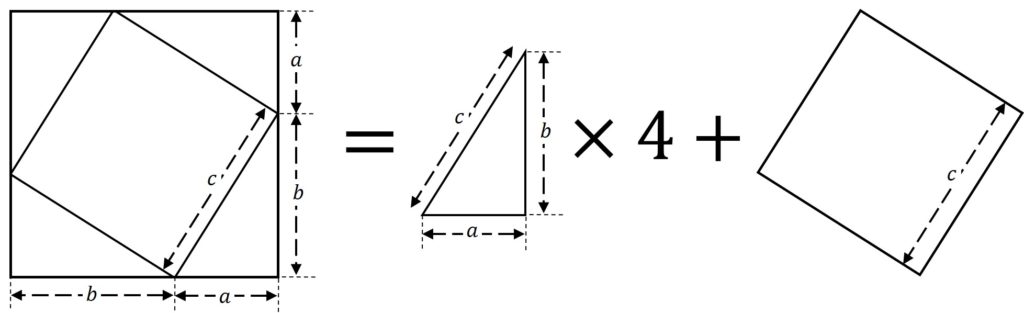
左の図は、長さ \( (a+b) \) の正方形の面積。
右の図は、底辺 \( a \)、高さ \( b \) からなる直角三角形4つと、長さ \( c \) の正方形の面積。
これらを計算すると、
\begin{eqnarray} (a+b)^2 &=& \frac{1}{2}ab \times 4 + c^2 \\ a^2+ 2ab+ b^2 &=& 2ab + c^2 \\ a^2+ b^2 &=& c^2 \end{eqnarray}
よって、三平方の定理が証明できた。
3.その他
よく使われる三角形の比
① 直角二等辺三角形
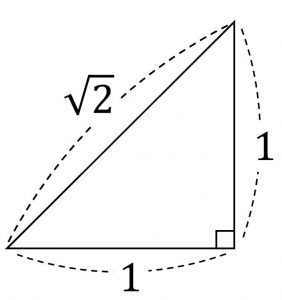
② \(30^{\circ},60^{\circ}\)のある直角三角形
