1次不等式
1.1次式の不等式
不等式とは
不等号を使って、数の大小関係を表した式を不等式という。
不等号の解き方
方程式と同じように求める事が出来ます。
※負の数でかけたり、負の数で割ると、不等号の向きが逆になる。
例)\(-2x+4>12\)を解く。
\(\begin{align}-2x+4 &\gt 12 \\ -2x &\gt 12 -4 \\ -2x &\gt 8 \\ x &\lt -4 \end{align}\)
文字を入れた不等式の解
① \(ax \gt b\)の解
\(a \gt 0の時、x \gt \frac{b}{a} , \quad a \lt 0 のとき \quad x\lt \frac{b}{a}\) \( a=0のとき \quad \begin{cases} b \geq 0 \quad ならば \quad 解なし \\ b \lt 0 \quad ならば \quad 実数全体\end{cases}\)
② \(ax \lt b\)の解
\(a \gt 0の時、x \lt \frac{b}{a} , \quad a \lt 0 のとき \quad x\gt \frac{b}{a}\) \( a=0のとき \quad \begin{cases} b \gt 0 \quad ならば \quad 実数全体 \\ b \leq 0 \quad ならば \quad 解なし\end{cases}\)
2.連立不等式
連立不等式とは
2つ以上の不等式を組み合わせたもの。
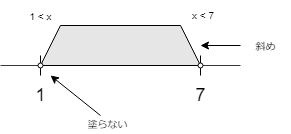
例1).\(x \gt 1 , \quad x\lt 7\)
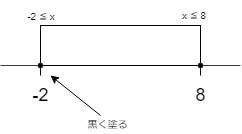
例2).\(x \geq -2 , \quad x \leq 8\)
3.絶対値記号を含む不等式
絶対値記号を含む不等式
① \(C \gt 0\)の時
\( |x| \lt C \Longleftrightarrow -C \lt x \lt C \) \( |x| \gt C \Longleftrightarrow x \lt -C \quad または \quad C \lt x \)
② \( |x|= \begin{cases} x \quad &(x\geq 0 のとき) \\ x \quad &(x\lt 0 のとき) \end{cases}\)
4.関連
問題 >> 方程式・基本問題3
