円の方程式
1.円の方程式
円の方程式
① \(中心(0,0),\quad 半径r\) の円
\(\quad x^2+y^2=r^2\)② \(中心(a,b),\quad 半径r\) の円
\(\quad (x-a)^2+(y-b)^2=r^2\)③ 一般式 \(x^2+y^2+ax+by+c=0\)
\(\quad (x+\frac{a}{2})^2+(y+\frac{b}{2})^2=\frac{a^2+b^2-4c}{4} \quad (a^2+b^2 \gt 4c)\) \(\quad 中心(-\frac{a}{2},-\frac{b}{2}),\quad 半径\frac{\sqrt{a^2+b^2-4c}}{2}\)
例題1
次の方程式の表す図形を求めよ。
① \(x^2+y^2-4x+2y-4=0\)
② \(x^2+y^2-2x+4y+3=0\)
③ \(x^2+y^2-6x+4y+10=0\)
解答①).
\(\quad x^2+y^2-4x+2y-4=0 \\
\quad (x-2)^2-4+(y+1)^2-1-4 =0 \\
\quad (x-2)^2+(y+1)^2 = 9 =3^2
\)
よって、中心(2,-1)、半径3の円の方程式となる。
解答②).
\(\quad x^2+y^2-2x+4y+5=0 \\
\quad (x-1)^2-1+(y+2)^2-4+5 = 0 \\
\quad (x-1)^2+(y+2)^2 = 0
\)
よって、点(1,-2)の方程式となる。
解答③).
\(\quad x^2+y^2-6x+4y+20=0 \\
\quad (x-3)^2-9+(y+2)^2-4+20 = 0 \\
\quad (x-3)^2+(y+2)^2 = -7
\)
よって解がないので、この方程式を表す図形はない。
2点を直径の両端とする円
2点 \((x_1,y_1),\quad(x_2,y_2)\)を直系の両端とする円
\(\quad (x-x_1)(x-x_1)+(y-y_1)(y-y_2) = 0\)
例題2
2点 \((1,4),\quad (3,6)\) を直系の両端とする円の方程式を求めよ。
解答).
\(\quad (x-1)(x-3)+(y-4)(y-6) =0 \\
\quad (x^2-4x+3)+(y^2-10x+24) = 0 \\
\quad (x-2)^2-4+3+(y-5)^2-25+24 = 0 \\
\quad (x-2)^2+(y-3)^2 = 2 = (\sqrt{2})^2
\)
よって、\(中心(2,5),半径\sqrt{2}\)
別解答).
2点の中心は
\(\quad (\frac{1+3}{2},\frac{4+6}{2}) = (2,5)\)となり、半径rの長さは直径の半分なので、
\(\quad \begin{align}
r &= \frac{\sqrt{(3-1)^2+(6-4)^2}}{2} \\
& = \frac{\sqrt{8}}{2} \\
& = \sqrt{2}
\end{align}\)
よって、求める円の方程式は
\(\quad (x-2)^2+(y-3)^2 = 2 = (\sqrt{2})^2\)
半円の方程式
\(r\)を半径とし、xy平面を考えるものとする。
① \(y = \pm \sqrt{r^2-x^2}\)
+ は円の上側、- は円の下側を表す。
これは\(\sqrt{a} \gt 0\)という範囲が理由となっている。
② \(x = \pm \sqrt{r^2-y^2}\)
+ は円の右側、- は円の左側を表す。
※これらは\(\sqrt{a} \gt 0\)という範囲が理由となっている。
例題3
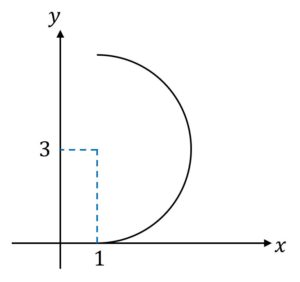
\(\quad 方程式 x=1+\sqrt{6y-y^2}\)のグラフを描け。
解答).
根号内を平方完成して
\(\quad x = 1+\sqrt{3^2-(y-3)^2}\)これは、中心 (1,3) の半径3の半円であるので、グラフは下図の通りになる。
