角と平行と多角形
1.角と平行線
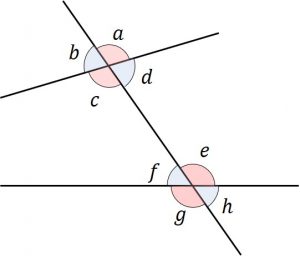
●対頂角 ・・・ 2直線が交わってできる4つの角のうち、向かい合いの2つの角。
組み合わせ:\(「\angle aと\angle c」,「\angle bと\angle d」,「\angle eと\angle g」,「\angle fと\angle h」\)
●同位角 ・・・ 2直線が他の1直線と交わってできる角のうち、1直線から見て同じ位置にある2つの角。
組み合わせ:\(「\angle aと\angle e」,「\angle bと\angle f」,「\angle cと\angle g」,「\angle dと\angle h」\)
●錯角 ・・・ 1直線が2直線に交わる時、1直線の反対側で相対する角。
組み合わせ:\(「\angle cと\angle e」,「\angle dと\angle f」\)
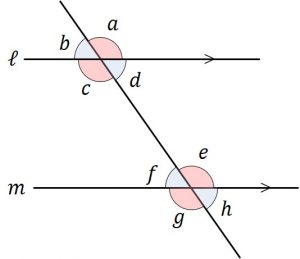
① 同位角が等しい。
② 錯角が等しい。
\(「\angle a = \angle c = \angle e = \angle g」,「\angle b = \angle d = \angle f = \angle h」\)
2.三角形の角
三角形の3つの内角の和は\(180^{\circ }\)である。
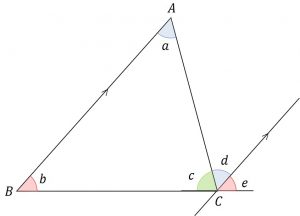
\(\triangle ABC \)の内角の和を求める。
\(辺BCをC方向に伸ばし、辺ABに平行で点Cを通る直線を描く。\)錯角の関係から、\(\angle a = \angle d\)、
同位角の関係から、\(\angle b = \angle e\)、
となり、
\(\begin{align}三角形の内角の和 &= \angle a + \angle b + \angle c \\ &= \angle d + \angle e + \angle c \\ &= 180^{\circ } \end{align}\)①鋭角三角形・・・全ての内角が90度以下の三角形。
②直角三角形・・・一つの内角が90度の三角形。
③鈍角三角形・・・一つの内角が90度以上の三角形。
3.多角形の角
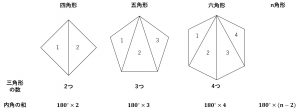
多角形の外角の和は\(360^{\circ }\)で一定である。
●最初に三角形で考える。
三角形の全ての線分の片方を下記の左図のように延長する。
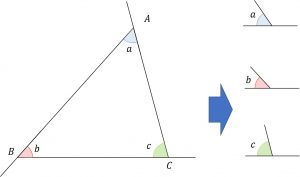
右の図のように、3つの角度について注目して考えればよい。
なので、三角形の外角の和は
\(\begin{align} (180^{\circ } – \angle a) + (180^{\circ } – \angle b) + (180^{\circ } – \angle c) &= 180^{\circ }\times 3 -(\angle a +\angle b +\angle c) \\ &= 180^{\circ }\times 3 – 180^{\circ } \\ &= 360^{\circ} \end{align}\)●次にn角形で考える。
三角形と同じように全ての線分の片方を延長する。
すると、nつの角度について注目して考えればよい。
なので、n角形の外角の和は
\( \begin{align} (180^{\circ } – \angle a_1) + (180^{\circ } – \angle a_2) + \dots + (180^{\circ } – \angle a_n) &= 180^{\circ }\times n -(\angle a_1 +\angle a_2 + \dots +\angle a_n) \\ &= 180^{\circ }\times n – 180^{\circ }\times (n-2) \\ &= 360^{\circ} \end{align} \)