三角形の五心
1.三角形の五心
三角形の五心
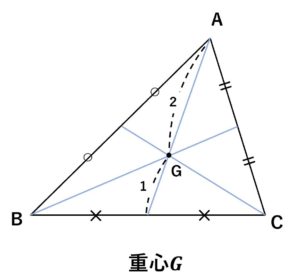
- 重心G:3つの抽選の交点。各中線は重心により、2:1に内分される。
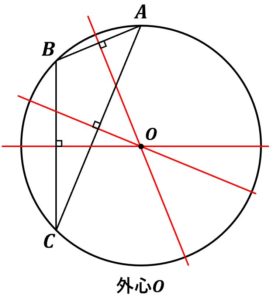
- 外心O:各辺の垂直2等分線の交点。三角形の外接円の中心。
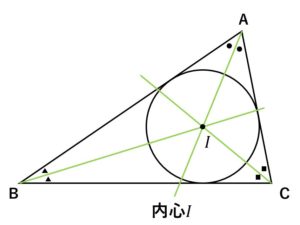
- 内心I:各内角の2等分線の交点。三角形の内接円の中心。
- 傍心I_a:1つの内角と他の2つの外角の2等分線の交点。傍心は3つあり、傍接円の中心。
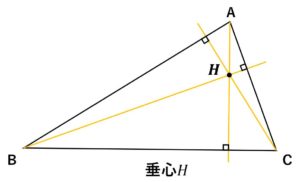
- 垂心H:各頂点から対辺におろした垂線の交点。

2.五心の関係性
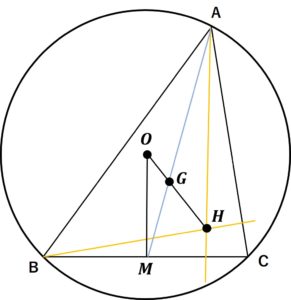
外心・垂心・重心の関係性
外心O、垂心H、重心G の関係は
\quad \quad AH = 2OM 3点O、G、Hは一直線上で \quad \quad GH = 2OG