数列と収束
0.数列と収束
自然界には、規則的に変化する現象がある。
それらの現象を理解するには数列の理解が不可欠である。
また数学では無限和、無限積で定義される関数や現象がある。
それらの関数、現象を扱うには
・どのような範囲
・どのような値
・最終的に行きつく値
を知る必要が出てくる。
1.数列
ある規則に従って並べられた数の列の事。
— 一般的な表し方 —
a_1,a_2,a_3,\cdots ,a_n,\cdots
または
\{ a_n \}
で表す。
また、 a_1 を初項、 a_2 を第2項
と呼び、 a_n を第 n 項または一般項と呼ぶ。
数列は自然数で定義されることが多いが、稀に a_{-3} 等、整数で定義されることもある。
上記でも述べたように、数列とは規則に従って並べられた数の列だが、
明確な場合
a_n = 5n ,\quad a_n = a_{n-1} r +2 ,\quad a_n = n^2
のように数式で表す。これを一般項と呼ぶ。
以下によくみられる数列を示す。
・等差数列
a_1 = a_1 ,\quad a_2 = a_1 +d ,\quad a_3 = a_1 + 2d , \cdots \cdots
・等比数列
a_1 = a_1 , \quad a_2 = a_1 r , \quad a_3 = a_1 r^2 , \cdots \cdots
・階差数列
ある数列 {b_n} がある時、この数列を差とする数列
a_1 = a_1 , \quad a_2 = a_1 + b_1 ,\quad a_3 = a_1 + b_1 + b_2 , \cdots \cdots
2.漸化式
以前の項との関係式を示す数列式の事。
上記で示した数列を漸化式で示してみる
・等差数列
a_n = a_{n-1} + d
・等比数列
a_n = a_{n-1} r
・階差数列
a_n = a_{n-1} + b_{n-1}
有名な漸化式では、フィボナッチ数列がある。
・フィボナッチ数列
a_1 = 1, \quad a_2 =1,\quad a_n = a_{n-1} + a_{n-2}
以下に、漸化式を数種類紹介しておく。
① 階差数列の形 a_{n+1} – a_n = f(n)
\begin{eqnarray} a_{n} = a_1 +\sum_{k=1}^{n-1} f(k) \quad (n \ge 2) \end{eqnarray}
② a_{n+1} = f(n)a_n
\begin{eqnarray} a_n = f(n-1)f(n-2) \cdots f(2)f(1)a_1 \end{eqnarray}
③ a_{n+1} = p a_n + q \quad (n=1,2,3,\cdots \cdots , ; p \neq 1,\quad q \neq 0 )
\alpha = p \alpha + q となる \alpha をとり、各辺を引くと
a_{n+1} – \alpha = p(a_n – \alpha)
と表せられるので、数列{ a_n – \alpha } は
公比p,\quad 初項(a_1 – \alpha) の等比数列となる
ゆえに、
a_n -\alpha = (a_1 -\alpha)p^{n-1}
④ a_{n+1} = pa_n + g(n) \quad (p \neq 0 )
両辺を p^{n+1} で割ると、
\frac{a_{n+1}}{p^{n+1}} – \frac{a_n}{p^n} = \frac{g(n)}{p^{n+1}}
ここで、 c_n = \frac{a_n}{p^n} , f(n) = \frac{g(n)}{p^{n+1}} と置くと
c_{n+1} – c_n = f(n) となり①の方法で解ける。
① a_1 = 1,\quad a_{n+1}=\frac{n}{n+1} a_n の数列 a_n を求めよ。
② a_1 = 1,\quad a_{n+1} = 3a_n + 2 の数列 a_n を求めよ。
③ a_1 = 1,\quad a_{n+1} = 3a_n + 3^{n+1} の数列 a_n を求めよ。
例題①).
a_n = \frac{n-1}{n}a_{n-1}
a_n = \frac{n-1}{n} \frac{n-2}{n-1} a_{n-2}
a_n = \frac{n-1}{n} \frac{n-2}{n-1}\frac{n-3}{n-2} \cdots \cdots \frac{1}{2} a_1 = \frac{1}{n}
例題②).
\alpha = 3\alpha +2 を与式から引くと、
a_{n+1} – \alpha = 3(a_n – \alpha)
a_{n+1} = 3a_n – 2\alpha となり、与式と比較して、 \alpha = -1
つまり、
a_{n+1} +1 = 3(a_n +1)
となり、 \{ a_n +1 \} の数列の初項は 2 、公比は 3 とわかるので、
a_n +1 = 2\cdot 3^{n-1}
∴ a_n = 2\cdot 3^{n-1} -1
例題③).
両辺を 3^{n+1} で割り、 c_n = \frac{a_n}{3^n} と置くと
c_{n+1} = c_n + 1
つまり、
c_n = c_1 + \sum_{k=1}^{n-1} 1
c_n = \frac{1_1}{3} + (n-1) = n-\frac{2}{3}
よって、 c_n = \frac{a_n}{3^n} なので、
a_n = 3^n (n-\frac{2}{3})
3.数列の和
数列の和 a_1 + a_2 + \cdots \cdots +a_n を \displaystyle \sum_{k=1}^{n} a_k と書く。
— 性質 —
(1). \displaystyle \sum_{k=1}^{n} (a_k + b_k) = \sum_{k=1}^{n} a_k + \sum_{k=1}^{n} b_k
(2). \displaystyle \sum_{k=1}^{n} c a_k = c \sum_{k=1}^{n} a_k
(3). \displaystyle \sum_{k=1}^{n} c = nc
※ c は定数。
(1). \displaystyle \sum_{k=1}^{n} k = 1 + 2 + \cdots + n = \frac{n(n+1)}{2}
(2). \displaystyle \sum_{k=1}^{n} k^2 = 1^2 + 2^2 + \cdots + n^2 = \frac{n(n+1)(2n+1)}{6}
(3). \displaystyle \sum_{k=1}^{n} k^3 = 1^3 + 2^3 + \cdots + n^3 = \{ \frac{n(n+1)}{2} \}^2
(4). \displaystyle \sum_{k=1}^{n} k^4 = 1^4 + 2^3 + \cdots + n^4 = \frac{1}{30}n(n+1)(2n+1)(3n^2+3n-1)
\displaystyle \sum_{k=1}^{n} (k+1)^3-k^3 の値を2通りの計算をする事で証明する。
\begin{eqnarray} \sum_{k=1}^{n} \{ (k+1)^3-k^3 \} &=& \sum_{k=1}^{n} ( k^3+3k^2+3k+1-k^3 ) \\ &=& \sum_{k=1}^{n}(3k^2+3k+1) \\ \end{eqnarray}
ここで左辺と右辺について、別々に式変形をする。
\begin{eqnarray} 左辺 &=& (2^3-1^3)+(3^3-2^3)+(4^3+3^3)+ \cdots +((n+1)^3+n^3) \\ &=& -1^3 + (2^3 – 2^3)+(3^3-3^3)+\cdots + (n^3-n^3) +(n+1)^3 = (n+1)^3-1 \\ \end{eqnarray} \begin{eqnarray} 右辺 &=& \sum_{k=1}^{n}(3k^2+3k+1) = \sum_{k=1}^{n} 3k^2 +\sum_{k=1}^{n} 3k + \sum_{k=1}^{n} 1 \\ &=& 3 \sum_{k=1}^{n} k^2 + 3\frac{1}{2}n(n+1) +n \\ \end{eqnarray}
次に、右辺=左辺として再計算して、目的の二乗の和を求める。
\begin{eqnarray} 3 \sum_{k=1}^{n} k^2 + \frac{3}{2}n(n+1) +n &=& (n+1)^3-1 \\ 3 \sum_{k=1}^{n} k^2 &=& (n+1)^3 – \frac{3}{2}n(n+1) – (n+1) \\ &=& \frac{(n+1)}{2} \{ 2(n+1)^2 -3n -2 \} \\ &=& \frac{(n+1)}{2}(2n^2 +n) \\ &=& \frac{1}{2}n(n+1)(2n +1) \\ \sum_{k=1}^{n} k^2 &=& \frac{1}{6}n(n+1)(2n +1) \\ \end{eqnarray}
となる。
— 他の累乗の和について —
同様に、3乗の和については
(k+1)^4 – k^4 の和について計算を行う
4乗の和については
(k+1)^5 – k^5 の和について計算を行う事で求めることが出来る。
この形になる数列の和の問題が多い。
4.数列の収束
数列 {a_n} が与えられ、 n \to \infty にした時、
特定の実数値 \alpha に近づくならば、
\lim_{n \to \infty} a_n = \alpha
と書き、 a_n は n を無限大に飛ばした時、
\alpha に収束するという。
上記の収束の説明は厳密ではない。
何故なら、
・無限大に飛ばすとは?
・無限大とはどれくらい大きくするのか?
・どんな値よりも大きい数?
・じゃあそれより大きい数では?
等と、無限大( \infty )とは非常に抽象的な表現である。
この収束を具体的に説明した証明法が下記で示す
\varepsilon – N 論法である。
極限を議論するのに、用いらられる証明法である。
「 \lim_{n \to \infty } a_n = \alpha 」
これを \varepsilon – N 論法で書き直すと、
↓
「 \forall \varepsilon , \exists N \in \mathbb{N} \quad s.t. \quad \forall n > N \to |a_n – \alpha | < \varepsilon 」
関連 >> 数学記号と意味
数学の記号が多くて、よくわからない方もいるかと思うので、
記号を使わずに答えると、
「任意の\varepsilonに対して、もし n が N より大きいなら、 |a_n – \alpha | < \varepsilon となる N が存在する。」
日本語に直しても分かりにくいですよね。
これを説明していきます。
「 \forall \varepsilon , \exists N \in \mathbb{N} \quad s.t. \quad \forall n > N \to |a_n – \alpha | < \varepsilon 」
この論法の厳密な所は、極限を議論するのに具体的に
「ものすごく大きな数字 ( n )」
と
「ものすごく小さな数字 ( \varepsilon )」
を設定できたところです。
では、どの辺りが設定できているのか解説していきます。
1. \exists N \in \mathbb{N},\quad \forall n > N
・特定の N
・それより大きい全ての n
大きい数の議論
A「ものすごく大きい N よりも大きい数字?」
B「いつでもAさんが考える数字 N よりも大きい数字 n だよ」
これでもの凄く大きな数字を設定できた。
2. \forall \varepsilon > 0
・0より大きい全ての \varepsilon
小さい数の議論
A「0より大きいかったら、どんだけ小さくてもいいの?」
B「どんだけ小さくてもいいですよー」
これでものすごく小さい数を設定できた。
※厳密には大きい数字も含んでいる。
ただこの論法で意味するところは、
めっちゃ小さい数を扱うという事です。
3. |a_n – \alpha | < \varepsilon
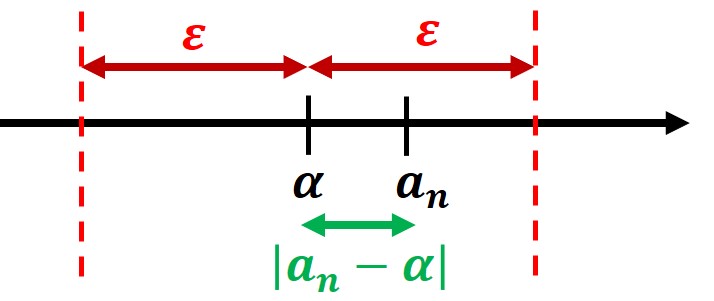
・ \alpha を中心に距離 \varepsilon 内に a_n が存在する。
収束の議論
A「ものすごく小さい \varepsilon 内に a_n があるの?」
B「そうだよ」
A「じゃあa_nってほぼほぼ\alphaじゃん」
このように厳密に大きい数と小さい数を議論できるのが、 \varepsilon – N 論法です。
そのため極限を議論出来るのです。
関連 >> \varepsilon – \delta 論法 (関数の極限)
5.無限級数の収束性
無限数列 {a_n} の各項を初項から無限に足し合わせた式を無限級数という。
\begin{align} a_1 + a_2 + \cdots + a_n + \cdots = \sum_{k=1}^{\infty} a_k \end{align}
無限数列 {a_n} の各項を初項から無限に足し合わせた式を無限級数という。
無限級数が S に収束する時、
\begin{align} \sum_{n=1}^{\infty} a_n = S \end{align}
と表す。
(1). 数列 {a_n} の無限級数が収束する時、
\begin{align} \lim_{n \to \infty } a_n = 0 \end{align}
数列 {a_n} は0に収束する。
(2) . 数列 {a_n} が収束する時、無限級数 \lim_{n \to \infty}S_nは収束するとは限らない。
(1)の証明
\sum_{n \to 1}^{\infty} a_n がSに収束する時、 n \ge 2 で
\begin{align} a_n = S_{n} – S_{n-1} \end{align}
であるから
\begin{align} \lim_{n \to \infty } a_n &= \lim_{n \to \infty } (S_{n} – S_{n-1}) \\ &= S-S \\ &=0 \end{align}
(2)の例
\begin{align} a_n = 1 + \frac{1}{n} \end{align}
この数列 a_n は \lim_{n \to \infty } a_n = 1 と収束するが、その級数は
\begin{align} \sum_{n=1}^{\infty} 1 + \frac{1}{n} = \infty \end{align}
と発散する。